Introduction
The qonvert package is part of the HQS Quantum Libraries, which contain the modules alqorithms, qonvert, noise-mapper and the bath-mapper, as shown in Figure 1.
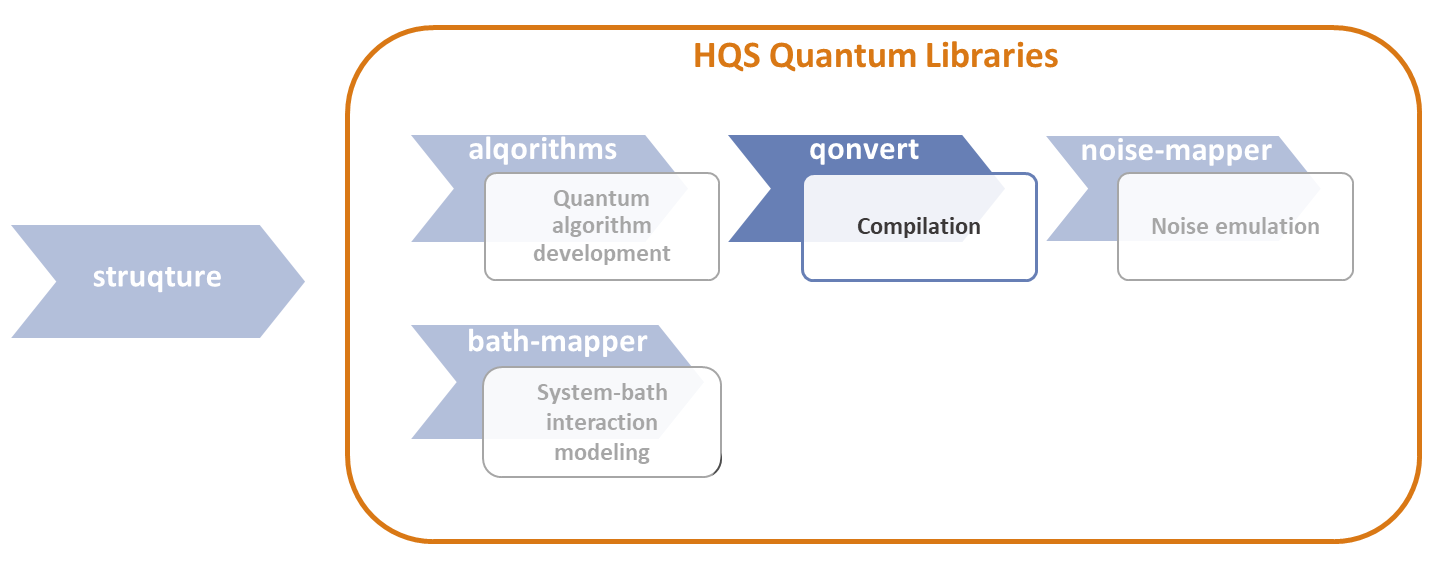
Figure 1: HQS Quantum Libraries - Qonvert
qonvert is the HQS compiler package, which offers comprehensive functionality for quantum circuit and quantum program optimization. It decomposes circuits into a given set of gates, optimizes them for efficiency, and introduces noise to emulate the behavior of physical quantum computers. Additionally, qonvert provides routing capabilities to further enhance circuit performance.
Applications
qonvert can be used to compile a Circuit or QuantumProgram to make it compatible with a chosen device whether it is for simulation purposes or to run on real quantum computing hardware. The compilation routine provides a range of functionality, such as gate decomposition, circuit optimization, noise insertion and routing. This last compilation step is necessary to account for limited connectivity, to increase performance and to properly represent characteristics of the quantum computing hardware.
Getting started
The package can be installed with the following command:
hqstage install pyqonvert
Please note that the HQS Quantum Libraries are currently only supported on Linux and MacOS.
Every Converter implements the convert method, offering a unified interface that takes as input
- circuits or quantum programs
- a
qoqo.devicesdevice - optionally, a noise model.
Output: The method ensures consistency and ease of use by returning the same type that was input—if a circuit is provided, a circuit is returned; if a quantum program is input, a quantum program is returned.
This straightforward design is powerful, enabling users to apply various conversions across circuits or programs with minimal code. For instance, the converters can be gathered in a list and called from within a for loop:
converters = [ ... optimizer, routers, decomposers, noise adders ... ]
for converter in converters:
circuit = converter.convert(circuit, device, noise_models)
To see qonvert in action, refer to the examples.
Features
HQS's qonvert offers a range of classes designed to "convert" quantum circuits and quantum programs, each serving as a Converter with specific functionalities:
- Gate Decomposition - enables the decomposition of single- and two-qubit gates into native gates supported by the quantum computing hardware.
- Noise Insertion - facilitates the insertion of decoherence noise through qoqo's
Pragmaoperations and introduces over-rotation noise via rotation gates. Note: qoqo is the open-source toolkit to represent quantum circuits by HQS Quantum Simulations. - Optimization - optimizes quantum circuits and quantum programs to enhance efficiency and performance.
- Routing - provides routing capabilities to address the challenge of limited qubit connectivity in quantum computing hardware.
HQS provides a comprehensive API documentation for all the functions availble in qonvert.
Gate decompositions: single- and two-qubit
Gate decomposition in quantum computing refers to the process of breaking down a gate into a set of single- and two-qubit gates. In general, the user will create a quantum circuit using a quantum algorithm, which is hardware-agnostic. While this quantum circuit can usually be simulated on many backends (e.g. qoqo-quest, qoqo-qiskit, qoqo-for-braket) without any recompilation, running it on a real quantum device requires adapting to the restricted set of natively available gates. Therefore, it is important to be able to decompose the gates present in the circuit into the gates available on the hardware. Additionally, different types of quantum computers have distinct set of native gate making decomposition even more essential.
Gate decomposition also plays a crucial role when modeling the noise of a quantum device. As noise often occurs during each gate operation, ensuring that the circuit contains the correct sequence of gates is vital for the correctness of the computation.
qonvert offers the SingleQubitGateDecomposer and TwoQubitGateDecomposer converters for this purpose. They are applied to circuits and quantum programs using the convert function.
Single-qubit gate decompositions
Functionality
The SingleQubitGateDecomposer converter decomposes any single-qubit gates into a set of specified single-qubit gates. It takes as input a quantum circuit or a quantum program and the device specifications, which specifies the available gate operations. The converter then matches the circuit's single-qubit gates with the operations supported by the device. If a single-qubit gate is not supported, the converter computes various possible decompositions, each weighted by their gate counts. Finally, the decomposition with the fewest gates is selected to replace the original gate in the circuit.
For details on the available decompositions, please refer to the Python API
Initalizing the SingleQubitGateDecomposer Class.
The SingleQubitGateDecomposer class is imported from the hqs_quantum_libraries.qonvert.decompositions module.
from hqs_quantum_libraries.qonvert.decompositions import SingleQubitGateDecomposer
# initialize noise inserter
decomposer = SingleQubitGateDecomposer()
# Ready to use for noise addition.
Example
We give an example to show the single-qubit decomposer's functionality. Figure 1 contains the resulting circuit.
from hqs_quantum_libraries.qonvert.decompositions import SingleQubitGateDecomposer
from qoqo import devices, Circuit
from qoqo import operations as ops
decomposer = SingleQubitGateDecomposer()
# Initialize device
number_qubits = 3
device = devices.AllToAllDevice(
number_qubits,
[
"RotateY",
"RotateZ",
"SqrtPauliX",
"InvSqrtPauliX",
],
[],
1.0,
)
# Initialize circuit
circuit = Circuit()
circuit += ops.DefinitionBit("ro", 1, True)
circuit += ops.CNOT(0, 1)
circuit += ops.CNOT(0, 2)
circuit += ops.Hadamard(0)
circuit += ops.MeasureQubit(0, "ro", 0)
# Decomposition
circuit = decomposer.convert(circuit, device, [])

Two-qubit gate decompositions
The TwoQubitGateDecomposer converter decomposes general two-qubit gates into native two-qubit gates and generic single-qubit gates. It takes a quantum circuit and the device specifications as input. The device specifies the available gate operations. The converter then matches the circuit's gates with the operations supported by the device. If a two-qubit gate is not supported, the converter explores various possible decompositions, each weighted by their gate counts. Finally, the decomposition with the fewest gates is selected to replace the original gate in the circuit.
For details on the available decompositions, please refer to the Python API
Initalizing the TwoQubitGateDecomposer Class.
The TwoQubitGateDecomposer class is imported from the hqs_quantum_libraries.qonvert.decompositions module.
from hqs_quantum_libraries.qonvert.decompositions import TwoQubitGateDecomposer
# initialize noise inserter
decomposer = TwoQubitGateDecomposer()
# Ready to use for noise addition.
Example
We provide an example to demonstrate the functionality of the two-qubit decomposer, as illustrated in Figure 2, which shows the resulting circuit. It is important to note that the two-qubit decomposer produces single-qubit rotation gates that may not be natively supported by the device. Therefore, in practice, it is essential to subsequently apply the single-qubit decomposition converter.
from hqs_quantum_libraries.qonvert.decompositions import TwoQubitGateDecomposer
from qoqo import devices, Circuit
from qoqo import operations as ops
decomposer = TwoQubitGateDecomposer()
# Initialize device
number_qubits = 3
device = devices.AllToAllDevice(
number_qubits,
[],
[
"CNOT",
"ControlledPauliZ",
"PhaseShiftedControlledZ",
],
1.0,
)
# Initialize circuit
circuit = Circuit()
circuit += ops.DefinitionBit("ro", 1, True)
circuit += ops.PauliX(0)
circuit += ops.SWAP(0, 1)
circuit += ops.Hadamard(0)
circuit += ops.MeasureQubit(0, "ro", 0)
# Decomposition
circuit = decomposer.convert(circuit, device, [])

Adding noise to a QuantumProgram or Circuit
Noise is an inherent part of real quantum systems, and simulating its effects is crucial for understanding the behavior of quantum algorithms in real-world conditions. The open source package qoqo provides users with several ways to define noise models precisely. The noise operations can be directly added to a quantum circuit and then be simulated by compatible backends.
Adding Decoherence
As decoherence noise does not translate into unitary quantum gates, the noise operations are defined as Pragma operations in qoqo. The strength of the noise is determined by defining a gate_time and a rate. The noise Pragma operations affect the system as a Lindblad type noise acting on the system with the rate rate for the time gate_time.
The Noise Models
Struqture lets users represent the decoherence part of the Lindblad equation using the struqture.spins.PlusMinusLindbladNoiseOperator class. The available noise models include:
-
ContinousDecoherenceModel: The noise model representing a continuous decoherence process on qubits. This noise model assumes that all qubits are constantly experiencing decoherence over time (e.g. due to coupling to the environment). The noise for each qubit can be different but only single-qubit noise is included in the model -
DecoherenceOnGateModel: This noise model for noise that is only present on gate executions. It adds noise when specific gates (identified by the name of the gate and qubits it acts on) are executed. -
DecoherenceOnIdleModel: The noise model which adds noise to qubits not involved in an operation, when that gate operation is executed (i.e. to the qubits which remain idle during the operation).
The NoiseInserter Converter
The NoiseInserter allows users to add noise Pragma operations to a given circuit or QuantumProgram, where the noise operations are derived from the input noise models. The noise model specifies the type of noise operations to be inserted, e.g. PragmaDamping, PragmaDephasing or PragmaDepolarizing as well as the rate of the noise. The gate time is inferred from the device being used.
The noise is added either before, after or symmetrical around gate operations present in the circuit. This is defined by the user when initializing the NoiseInserter.
Initializing the NoiseInserter Class
The NoiseInserter class is imported from the hqs_quantum_libraries.qonvert.noise module. The following values are needed to initialize it.
noise_mode: specifies the type of noise insertion. Allowed values includeactive_qubits_only- noisePragmas are added to the qubits involved in gate operations in the circuit.all_qubits- noisePragmas are added on all the qubits involved in the circuit.parallelization_blocks- noisePragmas are added to the qubits involved in the a parallel block marked byPragmaStopParallelBlockoperations in the circuit.
Additionally, there is the noise placement mode property of the NoiseInserter, which can be modified by the user. This setting determines whether noise is applied after, before, or symmetrically around (both before and after) a gate operation. By default, the noise placement mode is set to "After", meaning that all noise Pragma operations are sequentially added after gate operations in a circuit. You can modify this behavior using the functions provided below.
from hqs_quantum_libraries.qonvert.noise import NoiseInserter
noise_mode = "all_qubits"
# initialize noise inserter
noise_inserter = NoiseInserter(noise_mode)
# Ready to use for noise addition.
Noise placement modes
The following functions help in updating the noise placement mode:
noise_before_gate- noisePragmas are placed before each gate operation.
noise_inserter = NoiseInserter(noise_mode)
noise_inserter.noise_before_gate()
noise_symmetric_around_gate- noisePragmas are placed symmetrically around each gate operation.
noise_inserter = NoiseInserter(noise_mode)
noise_inserter.noise_symmetric_around_gate()
noise_after_gate- noisePragmas are placed after each gate operation.
noise_inserter = NoiseInserter(noise_mode)
noise_inserter.noise_after_gate()
Examples for each type of noise insertion
The NoiseInserter Class provides the convert method to insert noise into quantum circuits and QuantumPrograms.
The following example shows how one can insert noise according to a DecoherenceOnGateModel into a circuit with the "all_qubits" mode.
from hqs_quantum_libraries.qonvert.noise import NoiseInserter
from qoqo import devices, noise_models as nm, Circuit
from qoqo import operations as ops
from struqture_py.spins import PlusMinusLindbladNoiseOperator, PlusMinusProduct
noise_inserter = NoiseInserter("all_qubits").noise_before_gate()
decoherence_rate = 0.011
number_qubits = 2
# Initialize device and noise_model
device = devices.AllToAllDevice(
number_qubits,
["Hadamard"],
["CNOT"],
0.5
)
noise = PlusMinusLindbladNoiseOperator()
noise_product = PlusMinusProduct().z(0).plus(0)
noise.add_operator_product((noise_product, noise_product), 2.5)
noise_model = nm.DecoherenceOnGateModel().set_single_qubit_gate_error(
"Hadamard",
0,
noise
)
# initialize circuit
circuit = Circuit()
circuit += ops.Hadamard(0)
circuit += ops.CNOT(0,1)
# Add noise
circuit_noise = noise_inserter.convert(circuit, device, [noise_model])

The convert function is applied to a QuantumProgram in a similar fashion.
from hqs_quantum_libraries.qonvert.noise import NoiseInserter
from qoqo import devices, noise_models as nm, Circuit, QuantumProgram
from qoqo import operations as ops
from qoqo.measurements import PauliZProduct, PauliZProductInput
noise_inserter = NoiseInserter("active_qubits_only")
decoherence_rate = 0.011
number_qubits = 2
# Initialize device and noise_model
device = devices.AllToAllDevice(
number_qubits,
["Hadamard"],
["CNOT"],
0.5
)
noise_model = nm.ContinuousDecoherenceModel().add_damping_rate(
[0, 1],
decoherence_rate
)
# initialize program
circuit = Circuit()
circuit += ops.Hadamard(0)
circuit += ops.CNOT(0,1)
z_circuit = Circuit()
z_circuit += ops.DefinitionBit("ro_z", 1, is_output=True)
z_circuit += ops.PragmaRepeatedMeasurement("ro_z", 1000, None)
measurement_input = PauliZProductInput(1, False)
measurement = PauliZProduct(
constant_circuit = circuit,
circuits=[z_circuit],
input=measurement_input,
)
qp = QuantumProgram(measurement, [])
# Add noise
program_noise = noise_inserter.convert(qp, device, [noise_model])

A circuit that has been optimized using the CircuitParallelizer converter is interspersed with PragmaStopParallelBlock instances. Noise can be added to a parallelized circuit or QuantumProgram using the "parallelization_blocks" mode. More information about the CircuitParallelizer converter can be found here and in the Python API documentation.
from hqs_quantum_libraries.qonvert.noise import NoiseInserter
from qoqo import devices, Circuit, noise_models as nm
from qoqo import operations as ops
noise_inserter = NoiseInserter("parallelization_blocks")
decoherence_rate = 0.011
number_qubits = 2
# Initialize device
device = devices.AllToAllDevice(
number_qubits,
["Hadamard"],
[],
0.5
)
noise_model = nm.DecoherenceOnIdleModel().add_damping_rate(
[0, 1],
decoherence_rate
)
# initialize circuit
circuit = Circuit()
circuit += ops.Hadamard(0)
circuit += ops.PragmaStopParallelBlock([0], 0.5)
circuit += ops.Hadamard(1)
circuit += ops.PragmaStopParallelBlock([1], 0.5)
# Add noise
circuit_noise = noise_inserter.convert(circuit, device, [noise_model])
Adding Overrotation Noise
Overrotation noise refers to the arbitrary rotation of qubits due to background factors. qonvert facilitates the addition of such noise using the following noise model:
SingleQubitOverrotationOnGate: The noise model which places a rotation gate with a randomly distributed rotation angle after a specified gate operation. Through theSingleQubitOverrotationDescriptionclass, one can define the parameters of the Gaussian distribution (mean and standard deviation) from which the overrotation angle is sampled.
The SingleQubitOverrotationAdder converter
The purpose of SingleQubitOverrotationAdder is to add single-qubit rotation gates that simulate overrotation noise informed by a SingleQubitOverrotationOnGate model.
Initializing the SingleQubitOverrotationAdder Class
The SingleQubitOverrotationAdder class is imported from the hqs_quantum_libraries.qonvert.noise module.
seed: the(optional) seed for the random number generator. If a seed is not provided, a machine-generated seed is used.
from hqs_quantum_libraries.qonvert.noise import SingleQubitOverrotationAdder
# initialize SingleQubitOverrotationAdder without a seed
overrotation_adder = SingleQubitOverrotationAdder()
# initialize SingleQubitOverrotationAdder with a seed
overrotation_adder_seeded = SingleQubitOverrotationAdder(seed=42)
# Ready to use for noise addition.
Example
Like NoiseInserter, the SingleQubitOverrotationAdder Class has the convert function which adds overrotation noise to quantum circuits and QuantumPrograms.
from hqs_quantum_libraries.qonvert.noise import SingleQubitOverrotationAdder
from qoqo import devices, Circuit, noise_models as nm
from qoqo import operations as ops
# Initializing the converter
noise_inserter = SingleQubitOverrotationAdder(seed=1)
# noise model
rotation_gate = "RotateZ"
# Parameters for Gaussian distribution single-qubit gates
mean_single = 0.0
std_single = 1.0
overrotation_noise_description_single = nm.SingleQubitOverrotationDescription("RotateZ", mean_single, std_single)
# Parameters for Gaussian distribution two qubit gates
mean_two = 1.0
std_two = 2.0
overrotation_noise_description_two = nm.SingleQubitOverrotationDescription("RotateX", mean_two, std_two)
overrotation_noise = nm.SingleQubitOverrotationOnGate()
overrotation_noise = overrotation_noise.set_single_qubit_overrotation(
"Hadamard",
0,
overrotation_noise_description_single
)
overrotation_noise = overrotation_noise.set_two_qubit_overrotation(
"CNOT",
0,
1,
(overrotation_noise_description_two, overrotation_noise_description_two)
)
# Initialize device and noise_model
number_qubits = 2
device = devices.AllToAllDevice(
number_qubits,
["Hadamard"],
["CNOT"],
0.5
)
# initialize circuit
circuit = Circuit()
circuit += ops.Hadamard(0)
circuit += ops.CNOT(0,1)
# Add noise
circuit_noise = noise_inserter.convert(circuit, device, [overrotation_noise])

program_noise = noise_inserter.convert(quantum_program, device, [overrotation_noise])
Figure 3: Adding overrotation noise
Optimizing the QuantumProgram or Circuit
The pyqonvert package consists of a number of methods to optimize quantum circuits by reducing the number of gates in the circuit. These are packaged as Converters, hence applied using the convert function.
Available optimizers
IdentityRemover- optimizes a quantum circuit or QuantumProgram by eliminating gates that are identified as identity below a certain specified tolerance. This optimizer takesidentity_toleranceas an input.
# Initialization
optimizer = IdentityRemover(identity_tolerance=1e-9)
MultipleRotationGateSimplifier- optimizes a quantum circuit or QuantumProgram by adding up identical rotation gates in separate DecompositionBlocks.
# Initialization
optimizer = MultipleRotationGateSimplifier()
CircuitParallelizer- optimizes a quantum circuit or QuantumProgram by grouping operations into parallel execution blocks. Each parallel execution block is terminated by aPragmaStopParallelBlockoperation. The execution time of the parallel block is extracted from the properties of the input device.
# Initialization
optimizer = CircuitParallelizer()
SleepInserter- adds aPragmaSleepoperation before or after a gate, depending on the user specified placement mode. ThePragmaSleepwill only be added to gates that involve at least one qubit from the input of the SleepInserter and are of the gate type specified in the input.
# Initialization
optimizer = SleepInserter(
gates = ["PauliZ"],
involved_qubits = [0,1],
sleep_time = 2.5,
placement = "after"
)
placement is an optional argument set to "after" by default.
NumericSingleQubitMultiplier- optimizes a quantum circuit or a QuantumProgram by multiplying non-symbolic single-qubit-gates. As an argument, it takes inidentity_tolerancethat specifies a threshold below which gates are neglected as identity.
# Initialization
optimizer = NumericSingleQubitMultiplier(identity_tolerance=1e-9)
VirtualZGateReplacement- applies virtual Z gate optimization. Provided that the natural two-qubit gate is diagonal in the Z-basis, theconverterreplaces RotateZ gates by virtual changes (rotations) of the qubit basis in the XY-Plane. This is done by replacing gates corresponding to rotation in XY-Plane withRotateXYgate.
# Initialization
optimizer = VirtualZGateReplacement()
By default, the converter adds RotateZ gates at the end to undo the changes made to the qubit basis. This behavior can be modified by using the function apply_final_rotz
optimizer = VirtualZGateReplacement().apply_final_rotz(False)
Note that if RotateXY gate is available in the device, the user is not required to use the VirtualZGateReplacement converter. Simply running the gate decomposition routine produces the same effect as the optimizer.
Example
We give an example where we apply a series of optimizations on a quantum circuit.
from hqs_quantum_libraries.qonvert.optimization import (
IdentityRemover,
NumericSingleQubitMultiplier,
CircuitParallelizer,
)
from qoqo import devices, Circuit
from qoqo import operations as ops
# Initialize device
number_qubits = 2
device = devices.AllToAllDevice(
number_qubits, ["RotateZ", "RotateX", "SingleQubitGate"], ["CNOT"], 0.5
)
# Initialize circuit
circuit = Circuit()
circuit += ops.RotateZ(0, 1e-6)
circuit += ops.RotateZ(0, 0.5)
circuit += ops.RotateX(1, -1.0)
circuit += ops.RotateX(1, 2.0)
circuit += ops.CNOT(0, 1)
# List of converters
converters = [IdentityRemover(1e-5), NumericSingleQubitMultiplier(1e-5), CircuitParallelizer()]
# Optimizations
for converter in converters:
circuit = converter.convert(circuit, device, [])

Routing on a device
In many quantum computing architectures, not all qubits are directly connected, meaning that operations between distant qubits must be routed through intermediate qubits. This is accomplished by inserting SWAP operations between qubits in a circuit.
The SingleOperationSwapRouter Converter
qonvert provides the SingleOperationSwapRouter Converter that inserts SWAP operations into a quantum circuit or QuantumProgram to enable operations on devices with limited connectivity.
Initalizing the SingleOperationSwapRouter Class.
The SingleOperationSwapRouter class is imported from the hqs_quantum_libraries.qonvert.routing module.
Parameters
swap_back- if set toTrue, additional SWAP operations are inserted to retrieve the original layout.only_before_decomposition- if set toTrue, SWAPS are only inserted outside of decomposition blocks. This option comes in handy during noise mapping which extensively makes use of decomposition blocks. Naively routing together with noise mapping requires a large number of SWAPs contributing to additional complexity. To minimize the number of SWAPs and allow for remapping without disrupting noise mapping, SWAPs are strategically inserted only before decomposition blocks that involve one or two qubits. To learn more about noise mapping, refer to this research article.
Note that when using setting only_before_decomposition=True, not all operations in the circuit (especially decomposition blocks involving more qubits in the first place) are routed. For full routing, a second pass with swap_back=True is necessary.
from hqs_quantum_libraries.qonvert.routing import SingleOperationSwapRouter
# initialize converter
noise_inserter = SingleOperationSwapRouter(
swap_back=True,
only_before_decomposition=False,
)
# Ready to use for routing.
Examples
Here is a simple example showing the functionality of the routing converter.
from hqs_quantum_libraries.qonvert.routing import SingleOperationSwapRouter
from qoqo import devices, Circuit
from qoqo import operations as ops
router = SingleOperationSwapRouter(True, False)
# Initialize device
number_qubits = 3
device = devices.GenericDevice(number_qubits)
device.set_two_qubit_gate_time("CNOT", 0, 1, 1.0)
device.set_two_qubit_gate_time("CNOT", 1, 0, 1.0)
device.set_two_qubit_gate_time("CNOT", 1, 2, 1.0)
device.set_two_qubit_gate_time("CNOT", 2, 1, 1.0)
# initialize circuit
circuit = Circuit()
circuit += ops.CNOT(0,2)
circuit += ops.PragmaRepeatedMeasurement("ro", 10)
# Routing
circuit = router.convert(circuit, device, [])

The following example shows how only_before_decomposition flag functions.
from hqs_quantum_libraries.qonvert.routing import SingleOperationSwapRouter
from qoqo import devices, Circuit
from qoqo import operations as ops
router = SingleOperationSwapRouter(False, True)
# Initialize device
number_qubits = 3
device = devices.GenericDevice(number_qubits)
device.set_two_qubit_gate_time("CNOT", 0, 1, 1.0)
device.set_two_qubit_gate_time("CNOT", 1, 0, 1.0)
device.set_two_qubit_gate_time("CNOT", 1, 2, 1.0)
device.set_two_qubit_gate_time("CNOT", 2, 1, 1.0)
# Initialize circuit
circuit = Circuit()
map = {0: 2, 2:0}
circuit += ops.PragmaStartDecompositionBlock([0, 2], map)
circuit += ops.CNOT(0, 2)
circuit += ops.CNOT(2, 0)
circuit += ops.PragmaStopDecompositionBlock([0, 2])
circuit += ops.PragmaStartDecompositionBlock([0, 1, 2], {})
circuit += ops.CNOT(1, 2)
circuit += ops.PragmaStopDecompositionBlock([0, 1, 2])
# Routing
circuit = router.convert(circuit, device, [])

only_before_decomposition = True.
Examples
Ising Model Hamiltonian
We will consider the example of a 3-spin transverse Ising model Hamiltonian that we want to simulate on a noisy quantum device. The device is assumed to have a linear topology, with direct connectivity between qubits 0 and 1, and between qubits 1 and 2. The noise will be modeled using classes from the qoqo.noise_models module. By utilizing hqs_quantum_libraries.qonvert, we will generate a finalized circuit that can be run on the device.
The Hamiltonian takes the form
To begin, we import all the necessary packages
from hqs_quantum_libraries.qonvert.optimization import IdentityRemover, NumericSingleQubitMultiplier
from hqs_quantum_libraries.qonvert.decompositions import SingleQubitGateDecomposer, TwoQubitGateDecomposer
from hqs_quantum_libraries.qonvert.routing import SingleOperationSwapRouter
from hqs_quantum_libraries.qonvert.noise import NoiseInserter
from qoqo import devices, Circuit, noise_models as nm
from qoqo import operations as ops
from struqture_py.spins import PlusMinusProduct, PlusMinusLindbladNoiseOperator
Then, we create the quantum circuit representation of the time evolution given by the 3-spin Hamiltonian
# hamiltonian parameters
J = -0.5
h = 0.3
# Trotter timestep
t = 0.001
# Initialising the circuit for the hamiltonian simulation
circuit = Circuit()
circuit += ops.CNOT(0,1)
circuit += ops.RotateZ(1, J*t)
circuit += ops.CNOT(0,1)
circuit += ops.CNOT(1,2)
circuit += ops.RotateZ(2, J*t)
circuit += ops.CNOT(1,2)
circuit += ops.CNOT(0,2)
circuit += ops.RotateZ(2, J*t)
circuit += ops.CNOT(0,2)
circuit += ops.RotateX(0, h*t)
circuit += ops.RotateX(1, h*t)
circuit += ops.RotateX(2, h*t)
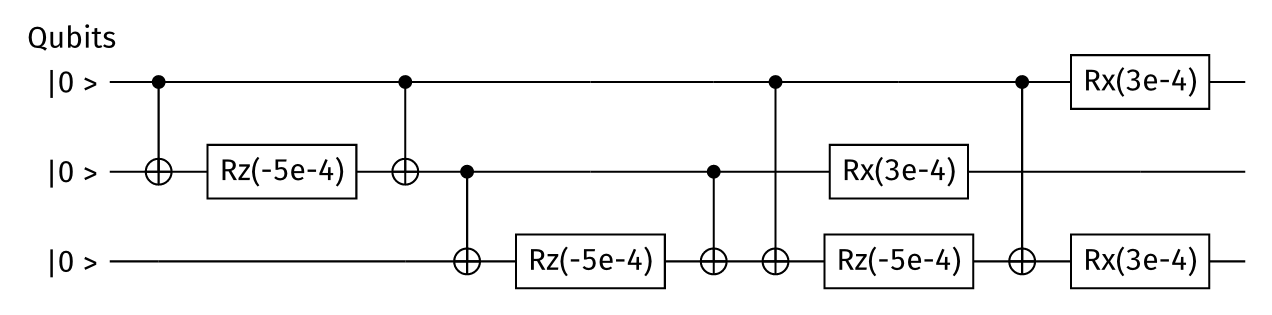 Figure 1: Circuit representing the time evolution of 3-spin Ising model Hamiltonian
We define the device specifications. We assume the device is connected linearly and that the available gates are
Figure 1: Circuit representing the time evolution of 3-spin Ising model Hamiltonian
We define the device specifications. We assume the device is connected linearly and that the available gates are RotateZ, RotateX, RotateY and CNOT.
# Device layout
# 0 --- 1 --- 2
# Initialising a device
number_qubits = 3
device = devices.GenericDevice(number_qubits)
# add single-qubit gates
for q in range(number_qubits):
device.set_single_qubit_gate_time("RotateZ", q, 1.0)
device.set_single_qubit_gate_time("RotateX", q, 1.0)
# add two-qubit gates
for q in range(number_qubits-1):
device.set_two_qubit_gate_time("CNOT", q, q+1, 1.0)
device.set_two_qubit_gate_time("CNOT", q+1, q, 1.0)
We also specify the noise model using struqture.spins.PlusMinusLindbladNoiseOperator and qoqo.noise_models. We assume there is decoherence on the CNOT gates and general continuous decoherence on all the qubits in the circuit, represented by a DecoherenceOnGateModel and a ContinuousDecoherenceModel ,respectively.
# Initialising noise models
noise_product_1 = PlusMinusProduct().z(1).plus(1)
noise_1 = PlusMinusLindbladNoiseOperator()
noise_1.add_operator_product((noise_product_1, noise_product_1), 0.05)
noise_product_2 = PlusMinusProduct().z(2).plus(2)
noise_2 = PlusMinusLindbladNoiseOperator()
noise_2.add_operator_product((noise_product_2, noise_product_2), 0.025)
on_gate_noise = nm.DecoherenceOnGateModel()
on_gate_noise = on_gate_noise.set_two_qubit_gate_error(
"CNOT", 0, 1, noise_1
)
on_gate_noise = on_gate_noise.set_two_qubit_gate_error(
"CNOT", 1, 2, noise_2
)
decoherence_rate = 0.005
continuous_noise = nm.ContinuousDecoherenceModel().add_damping_rate([0, 1, 2], decoherence_rate)
noise_models = [on_gate_noise, continuous_noise]
To run the circuit on a quantum device, we need to apply a series of converters. First, we initialize the SingleOperationSwapRouter, which handles routing to overcome the device's limited connectivity. Next, the TwoQubitGateDecomposer decomposes two-qubit gates into the device's native gates—in this case, CNOT gates—along with generic single-qubit rotations. The NumericSingleQubitMultiplier optimizes the circuit by combining single-qubit gates where possible, and the SingleQubitGateDecomposer further breaks down these gates into the device's allowable operations. The IdentityRemover then cleans up the circuit by removing any redundant single-qubit gates that simplify to identity operations after these conversions. Finally, the circuit is ready for noise addition, which is handled by the NoiseInserter, adding noise Pragmas to the circuit. We store the converters sequentially in a list.
# Initialising the converters
converters = [
SingleOperationSwapRouter(True, False),
TwoQubitGateDecomposer(),
NumericSingleQubitMultiplier(1e-9),
SingleQubitGateDecomposer(),
IdentityRemover(1e-9),
NoiseInserter("active_qubits_only"),
]
The converters are then effortlessy applied by iterating over them in a for loop,
for converter in converters:
circuit = converter.convert(circuit, device, noise_models)