Examples

Ising Model Hamiltonian

We will consider the example of a 3-spin transverse Ising model Hamiltonian that we want to simulate on a noisy quantum device. The device is assumed to have a linear topology, with direct connectivity between qubits 0 and 1, and between qubits 1 and 2. The noise will be modeled using classes from the qoqo.noise_models module. By utilizing pyqonvert, we will generate a finalized circuit that can be run on the device.

The Hamiltonian takes the form \[ H = \sum_{\langle i,j \rangle} J_{ij} \sigma^z_i \sigma^z_j + \sum_i h_i \sigma^x. \]

To begin, we import all the necessary packages

from pyqonvert.optimization import IdentityRemover, NumericSingleQubitMultiplier
from pyqonvert.decompositions import SingleQubitGateDecomposer, TwoQubitGateDecomposer
from pyqonvert.routing import SingleOperationSwapRouter
from pyqonvert.noise import NoiseInserter
from qoqo import devices, Circuit, noise_models as nm
from qoqo import operations as ops
from struqture_py.spins import PlusMinusProduct, PlusMinusLindbladNoiseOperator

Then, we create the quantum circuit representation of the time evolution given by the 3-spin Hamiltonian

# hamiltonian parameters
J = -0.5
h = 0.3
# Trotter timestep
t = 0.001
# Initialising the circuit for the hamiltonian simulation
circuit = Circuit()
circuit += ops.CNOT(0,1)
circuit += ops.RotateZ(1, J*t)
circuit += ops.CNOT(0,1)
circuit += ops.CNOT(1,2)
circuit += ops.RotateZ(2, J*t)
circuit += ops.CNOT(1,2)
circuit += ops.CNOT(0,2)
circuit += ops.RotateZ(2, J*t)
circuit += ops.CNOT(0,2)
circuit += ops.RotateX(0, h*t)
circuit += ops.RotateX(1, h*t)
circuit += ops.RotateX(2, h*t)

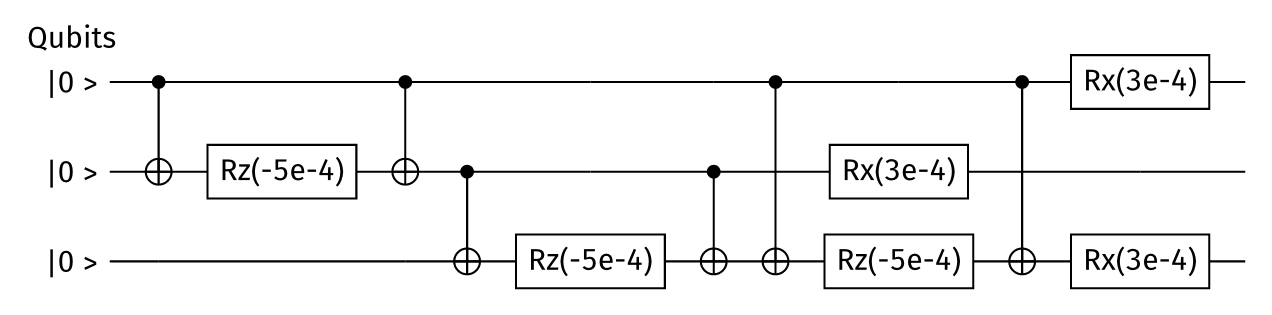Figure 1: Circuit representing the time evolution of 3-spin Ising model Hamiltonian We define the device specifications. We assume the device is connected linearly and that the available gates are RotateZ, RotateX, RotateY and CNOT.

# Device layout
#  0 --- 1 --- 2
# Initialising a device
number_qubits = 3
device = devices.GenericDevice(number_qubits)

# add single-qubit gates
for q in range(number_qubits):
    device.set_single_qubit_gate_time("RotateZ", q, 1.0)
    device.set_single_qubit_gate_time("RotateX", q, 1.0)

# add two-qubit gates
for q in range(number_qubits-1):
        device.set_two_qubit_gate_time("CNOT", q, q+1, 1.0)
        device.set_two_qubit_gate_time("CNOT", q+1, q, 1.0)

We also specify the noise model using struqture.spins.PlusMinusLindbladNoiseOperator and qoqo.noise_models. We assume there is decoherence on the CNOT gates and general continuous decoherence on all the qubits in the circuit, represented by a DecoherenceOnGateModel and a ContinuousDecoherenceModel ,respectively.

# Initialising noise models
noise_product_1 = PlusMinusProduct().z(1).plus(1)
noise_1 = PlusMinusLindbladNoiseOperator()
noise_1.add_operator_product((noise_product_1, noise_product_1), 0.05)

noise_product_2 = PlusMinusProduct().z(2).plus(2)
noise_2 = PlusMinusLindbladNoiseOperator()
noise_2.add_operator_product((noise_product_2, noise_product_2), 0.025)

on_gate_noise = nm.DecoherenceOnGateModel()
on_gate_noise = on_gate_noise.set_two_qubit_gate_error(
    "CNOT", 0, 1, noise_1
)
on_gate_noise = on_gate_noise.set_two_qubit_gate_error(
    "CNOT", 1, 2, noise_2
)

decoherence_rate = 0.005
continuous_noise = nm.ContinuousDecoherenceModel().add_damping_rate([0, 1, 2], decoherence_rate)
noise_models = [on_gate_noise, continuous_noise]

To run the circuit on a quantum device, we need to apply a series of converters. First, we initialize the SingleOperationSwapRouter, which handles routing to overcome the device's limited connectivity. Next, the TwoQubitGateDecomposer decomposes two-qubit gates into the device's native gates—in this case, CNOT gates—along with generic single-qubit rotations. The NumericSingleQubitMultiplier optimizes the circuit by combining single-qubit gates where possible, and the SingleQubitGateDecomposer further breaks down these gates into the device's allowable operations. The IdentityRemover then cleans up the circuit by removing any redundant single-qubit gates that simplify to identity operations after these conversions. Finally, the circuit is ready for noise addition, which is handled by the NoiseInserter, adding noise Pragmas to the circuit. We store the converters sequentially in a list.

# Initialising the converters
converters = [
    SingleOperationSwapRouter(True, False),
    TwoQubitGateDecomposer(),
    NumericSingleQubitMultiplier(1e-9),
    SingleQubitGateDecomposer(),
    IdentityRemover(1e-9),
    NoiseInserter("active_qubits_only"),
]

The converters are then effortlessy applied by iterating over them in a for loop,

for converter in converters:
    circuit = converter.convert(circuit, device, noise_models)