Use cases

The HQStage Modules are centered around solving quantum mechanical systems. HQStage provides access to a wide range of example systems and Hamiltonians. There is great interest in solving these systems and Hamiltonains on quantum computers.

HQStage examples and modules will be available for three use cases:

Nuclear magnetic resonance
Electron spectroscopy
Magnetic response

As of now we have published the nuclear magnetic resonance (NMR) use case. Electron spectroscopy and magnetic resonance use cases will be published later in 2025.

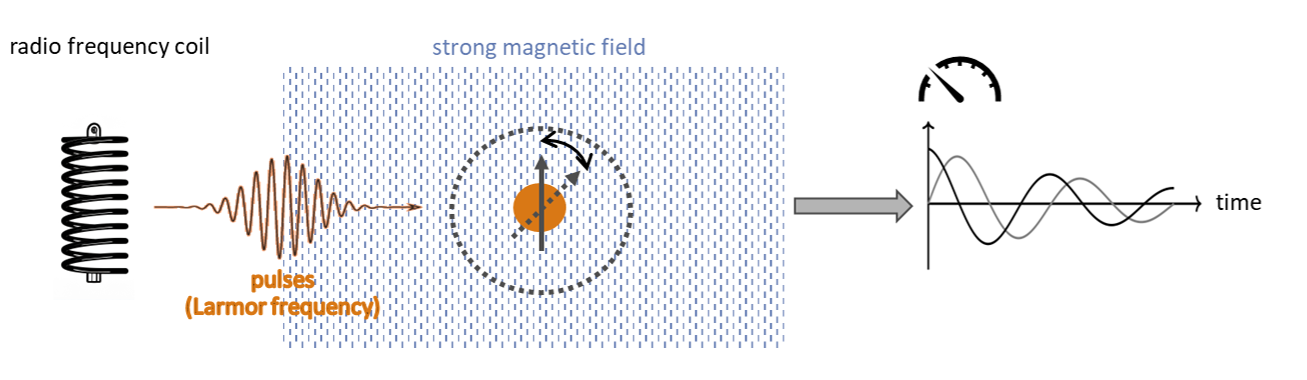
Nuclear magnetic resonance

Expert users in NMR spectroscopy should use our HQStage modules HQS Spectrum Tools. To get a feeling for NMR spectroscopy try out our end-to-end product HQSpectrum.

In the following we will naswer the question why NMR is a good use case for quantum computers. For this we use our ITBQ use case evaluation.

I. Identify industry problem. NMR is a routine, cornerstone analytical technique for chemistry and pharma, used to determine molecular structure and to quantify mixtures (qNMR). Spectra encode structure through chemical shifts and J‑couplings, which depend on molecular environment (solvent, temperature, pH, field strength) and can be complex, especially for 1H spectra and at lower magnetic fields (benchtop devices).

Principles of an NMR spectrometer. — Fig 1 Principles of an NMR spectrometer: the sample is placed in a strong magnetic field, causing a net magnetization of the nuclear spins by the static field. Pulses from radio frequency coils, in resonance with the Larmor frequency of the nuclei, cause an oscillating transverse magnetization. Measurement of the decaying response after completion of the pulse sequence leads to the NMR spectrum after processing.

Reliable analysis increasingly needs quantum‑mechanical spectrum simulations, but exact spin‑system simulations scale exponentially and require accurate parameters (shifts/couplings) that must be predicted or fitted. Industrial tasks: structure elucidation in solution and quantitative mixture analysis for quality control, metabolomics, and process monitoring—both demand consistent parameter assignment, handling conformers, and integration with existing NMR workflows and libraries. Net assessment: a strong, practical need for accurate, automated, end‑to‑end NMR simulation integrated into current tools, rated as a four‑out‑of‑five‑star industry problem (★★★★☆).

II. Transform to quantum. In the “transform to quantum” step we map molecules onto a quantum-mechanical spin model in which each nucleus is a spin-1/2 in a static magnetic field, and the spectrum is governed by Zeeman terms corrected by chemical shifts and by scalar J-couplings between spins; for diamagnetic molecules in liquids, direct dipolar couplings average out with molecular motion, while for macromolecules/solids they can matter. The resulting model is the Spin Hamiltonian:

\hat{H} = - k \sum γ_{k} (1 + δ_{k}) B \cdot I_{k} + 2 π k > l \sum J_{k l} I_{k} \cdot I_{l}

Operationally, the transformation proceeds by generating 3D geometries and relevant conformers from molecular structure, optimizing them, computing shieldings and J-couplings (e.g., via DFT), Boltzmann-averaging parameters over the conformer ensemble, and converting shieldings to chemical shifts for use in the Hamiltonian; while these procedures are established and largely automated, integration into analysis workflows and accurate treatment of environmental effects still require manual checks. In HQS Spectrum Tools we provide a collection of pre-calculated spin models for a range of molecules with different size and chemical structures. Use these as a starting point for your NMR calculations - classical or on quantum computers. Rating: ★★★★☆.

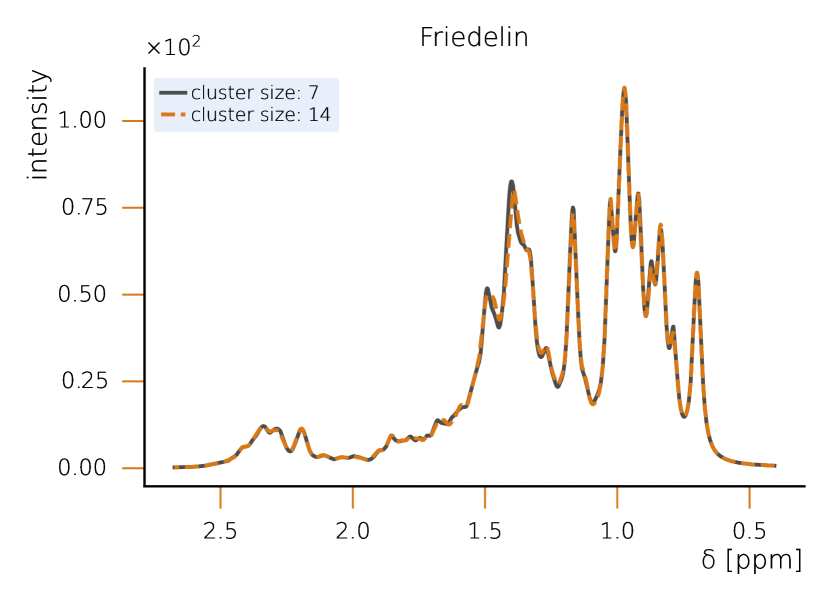
III. Get the job done without the quantum computer. This section sets a clear classical baseline for quantum advantage in NMR simulations. Exact NMR dynamics scales exponentially with the number of spins, but with HQS Spectrum Tools practical, accurate results are routinely achieved by combining spin‑clustering (grouping strongly interacting spins) with symmetry reductions (e.g., local SU(2)), as implemented in the HQS Spectrum Tools and benchmarked against Spinach. Under typical high‑field conditions, these methods compute 1H spectra for organic molecules with tens of protons in minutes; for example, a 50‑spin Friedelin spectrum converges with clusters of about 8–12 spins. When correlations extend across the whole molecule, simple clustering can miss key features, yet symmetry‑aware exact modes still reproduce spectra for medium‑size systems, as shown for the 22‑spin 1,2‑di‑tert‑butyl‑diphosphane.

Net result: conventional tools already “get the job done” for most NMR scenarios and provide unambiguous, automation‑friendly benchmarks (★★★★★). Quantum hardware is expected to add value mainly in low‑field or densely coupled regimes where long‑range correlations make classical scaling prohibitive; the overall prospect for quantum advantage is rated high but not universal (★★★★☆).

IV. NMR spectral prediction reduces to tracking the time‑dependent transverse magnetization of an N‑spin system, expressed as

⟨ I^{x} (t)⟩ = Tr [I^{x} ρ (t)]

On classical hardware, exact simulation evolves the full

2^{N} ? t im es 2^{N}

density matrix, which scales exponentially with N according to the Liouville–von Neumann equation:

\frac{d}{d t} ρ (t) = - i [H, ρ (t)]

Quantum computers avoid this bottleneck by natively implementing unitary dynamics with N qubits:

ρ (t) = e^{- i H t} ρ (0) e^{+ i H t}

Standard NMR preparation rotates equilibrium magnetization into the transverse plane (e.g., a

\frac{π}{2}

pulse so that

ρ (0) \propto I^{y}

at low temperature), allowing the signal to be expressed as a sum over

I^{y}

eigenstates:

⟨ I^{x} (t)⟩ \propto m_{j}^{y} \sum m_{j}^{y} ⟨ m_{j}^{y} ∣ e^{i H t} I^{x} e^{- i H t} ∣ m_{j}^{y} ⟩

A quantum processor realizes this workflow by preparing

∣ m_{j}^{y} ⟩

, evolving under the Hamitlonian (e.g., via Trotterization or related simulators), and measuring

I^{x}

, requiring only polynomial sampling instead of storing an exponentially large density matrix. The upshot is a concrete route to quantum advantage in precisely the difficult regimes for classical methods—large, highly entangled spin networks, strong long‑range couplings, and low‑field conditions—while remaining aligned with standard NMR pulse logic and measurements.

While quantum computing offers an exponential advantage for NMR simulations, classical algorithms have also been developed to efficiently treat large spin systems. One particularly effective approach is spin clustering (see Fig. (2)), which reduces computational complexity by grouping strongly interacting spins together, enabling approximate solutions. In many cases, especially at high magnetic fields, this method can provide accurate results with cluster sizes of 8–12 spins, even for complex molecules. For example, in the case of Friedelin (Fig. 2), a 50-spin molecule, the cluster-based solver shows good convergence, with minimal spectral changes as the cluster size increases. This demonstrates that for certain systems with relatively weak spin correlations, spin clustering provides a feasible classical approach.

However, when strong correlations extend across the system, as in the case of 1,2-di-tert-butyl-diphosphane (Fig. 2), the limitations of spin clustering become apparent. This molecule consists of 22 coupled spins, where cluster approximations cannot fully capture the spin interactions. Instead, solving the system exactly requires the exploitation of local SU(2) symmetry, which significantly reduces the computational complexity while maintaining full accuracy. Without symmetry considerations, the problem would require the diagonalization of a $2^{22} \times 2^{22}$ -dimensional matrix, making classical exact diagonalization basically intractable. Given examples like 1,2-di-tert-butyl-diphosphane, it seams likely that parameters example and parameter regimes exist in which classical solutions remain challenging. At the same time it is clear that classical solvers can cover a large part of the relevant cases for NMR. Therefore we rate the probability to achieve quantum advantage with four stars (★★★★★).

Keyboard shortcuts

HQStage Documentation

Use cases

Nuclear magnetic resonance