HQS Noise Mapper

The HQS Noise Mapper is a module that can be used in conjunction with other Quantum Libraries by HQS Quantum Simulations GmbH.

The HQS Noise Mapper provides a method for analyzing the effects of noise in quantum circuits, specifically those designed to simulate the time evolution of quantum spin systems through Trotterization. This method helps to understand the extent of noise effects and provides a good approximation to the actual dynamics of the noisy quantum circuit.

Overview

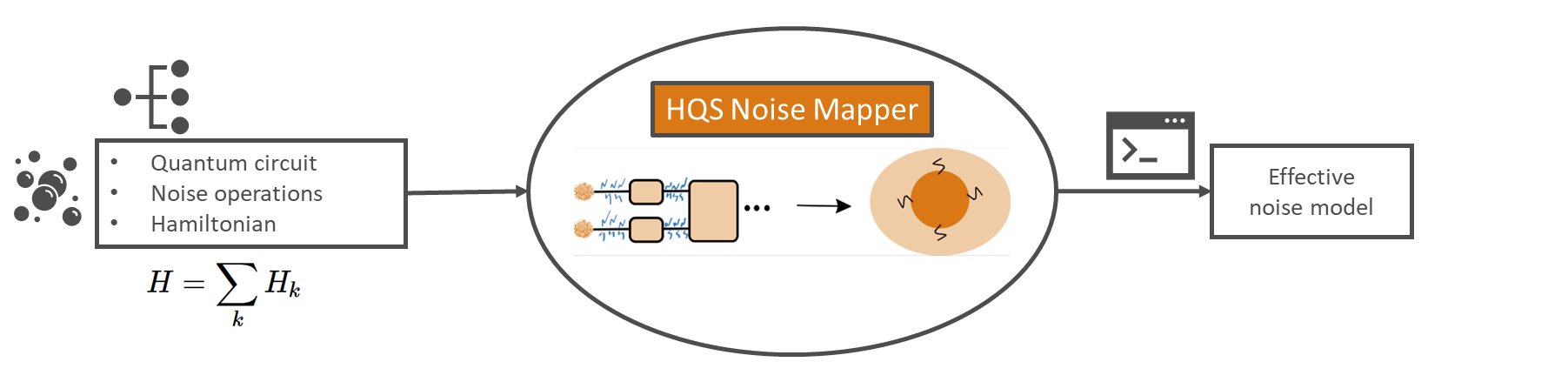
The primary goal of the HQS Noise Mapper is to calculate the noisy algorithm model that would effectively be correspond to running on a given noisy hardware device. Based on the input noisy quantum circuit corresponding to one time step, the output of the HQS Noise Mapper tool is the sum of all effective noise terms, corresponding to the Lindblad noise operator of the noisy algorithm model.

Why it is useful

Time evolution of quantum systems is widely discussed as one of the prime applications of quantum computers due to the exponential speedup these devices promise over conventional computers. However, present-day universal quantum computing hardware is subject to errors (so-called “noise”), which are yet to be overcome. In order to enable useful, near-term quantum computing, it is crucial to understand the effects that noise can have on the results of a run performed on such a device.

The HQS Noise Mapper implements models to utilize the noise of the available devices to enable useful, near-term quantum computing. More specifically, it implements noise mapping, which is the construction of a static noisy algorithm model based on a quantum circuit and physical noise on a quantum computer. For further details on the scientific background of this method, please refer to the background section or our recent paper: arXiv:2210.11371.

Functionality

The HQS Noise mapper implements the noisy algorithm model. This is the static noise model that determines the effective time propagation when a quantum algorithm for the coherent time propagation under a Hamiltonian is run on a quantum computer with physical noise. In particular, the following functions are provided:

  • noisy_algorithm_model: returns the full noisy algorithm model including coherent terms. It takes as input the annotated circuit of one Trotter step, the original Hamiltonian, and the Trotter timestep.

  • noisy_algorithm_model_pure_noise: provides noise-mapping functionality but only returns the effective noise part of the noisy algorithm model. It does not require the Hamiltonian as input.

Conditions

  • Noise mapping works when the quantum algorithm under consideration is fundamentally of the Trotterization type.
  • The noisy algorithm model can be extracted from a quantum circuit that represents one Trotter step.
  • The noise mapper accepts circuits that have already been fully compiled for the target architecture and annotated with the necessary meta information.
  • Two forms of metadata annotation are required to apply noise mapping:
    1. Marking the decomposition blocks, which are the parts of the circuit that correspond to implementing a partial time propagation under a \(H_k\).
    2. Information about the physical noise.
  • The noise mapping in the Noise Mapper is based on the assumption that the Trotter time-step \(t\) is short enough with respect to the Lindblad terms.

Please refer to the background section for more details.

Use cases

The HQS Noise Mapper is designed to help users understand the effects of noise in quantum circuits.

  • Understand device noise: It helps users to better understand the noise that the device actually experiences.

    • This can be used for example for device characterization, i.e. to accurately simulate what actually happens on the device to describe and characterize it, aiding in testing and improvement during the development life cycle.
    • Simulating noisy quantum computers can be also beneficial for benchmarking experimental results.

  • Time evolution: Apply time evolution on the circuit with the effective noise model to get the time-evolved matrix and probabilities to study the dynamics of an open quantum system.

  • Algorithm selection: Choose which algorithm to use when running a quantum program on a given device by analyzing which algorithm leads to less noise. The different algorithms can be found in the HQS Quantum Library alqorithms.

  • Analyzing noise for NMR simulations: Extract line width to predict how precise a noisy quantum computer can simulate NMR spectra.

Further applications

Please note that HQS Noise Mapper is intented to be used in conjunction with the open source libraries qoqo and struqture by HQS Quantum Simulations GmbH.

  • The output of the HQS Noise Mapper is a struqture object called SpindLindbladNoiseSystem, representing the effective noise model. The output can be utilized with the quantum toolbox QuTiP to study the time evolution of relevant observables via the available struqture-qutip-interface provided by HQS Quantum Simulations GmbH.

  • Additionally, the SpinLindbladNoiseSystem object can be used to obtain an approximate time evolution beyond mean-field approximations, enabling the simulation of large systems.

Further reading

The scientific background of this method has been published in a recent paper: arXiv:2210.11371.

Examples

Users can find detailed examples in the Examples section.

API documentation

The noise mapper provides several interface functions for workflows and job run definitions. A detailed description can be found in the Python API documentation.

Background

The HQS Noise Mapper implements models to utilize the noise of the available devices to enable useful, near-term quantum computing. In particular, it implements noise mapping, the construction of a static noisy algorithm model based on a quantum circuit and physical noise on a quantum computer, as described in this section.

The noisy algorithm model is the static noise model that determines the effective time propagation when a quantum algorithm circuit of the coherent time propagation under a Hamiltonian is run on a quantum computer with physical noise. The scientific background of this method has been published in a recent paper: arXiv:2210.11371, where we consider the extent to which a noisy quantum computer is able to simulate the time evolution of a quantum spin system in a faithful manner. In this section we describe the specific set of assumptions about the noise of the device and the technical details of the implemented noise mapping.

Conditions

Noise mapping works when the quantum algorithm under consideration is fundamentally of the Trotterization type, meaning that the original Hamiltonian can be written as a sum of local Hamiltonians \[ H = \sum_k H_k \[ H = \sum_k H_k \] and the time propagation under each \(H_k\) is given by a well-defined sequence of native quantum gates. The noisy algorithm model can be extracted from a quantum circuit that represents one Trotter step in a Trotterized time-propagation algorithm.

To be as general as possible, the noisy-algorithm extraction does not construct this quantum circuit that propagates a state for a virtual time. The noise mapper accepts circuits that have already been fully compiled for the target architecture and annotated with the necessary meta-information.

Two forms of metadata annotation are required to apply noise mapping:

  1. Marking the decomposition blocks, which are the parts of the circuit that correspond to implementing a partial time propagation under a \(H_k\)
  2. Information about the physical noise

For further details on the usage of the associated functionalities, please refer to the functionalities section of this documentation.

Noise Mapping

The noise mapping in the Noise Mapper is based on the assumption that the Trotter time-step \(t\) is short enough with respect to the Lindblad terms \(\mathcal{L}_1\) and \(\mathcal{L}_2\), and that the following equation is respected. \[ \exp(\mathcal{L}_1 t) \exp(\mathcal{L}_2 t) \approx \exp(\mathcal{L}_2 t) \exp(\mathcal{L}_1 t) \approx \exp((\mathcal{L}_1 + \mathcal{L}_2) t) \]

where \(\exp(\mathcal{L} t)\) is shorthand for applying the full time propagation under the Lindblad terms for time \(t\).

Functionality

Please note that HQS Noise Mapper is intented to be used in conjunction with other quantum computing libraries by HQS Quantum Simulations GmbH, especially the open source libraries qoqo and struqture.

HQS Noise Mapper provides the following functions:

  • noisy_algorithm_model which returns the full noisy algorithm model including coherent terms. It takes as input the annotated circuit of one Trotter step, the original Hamiltonian and the Trotter time-step.
  • noisy_algorithm_model_pure_noise also provides noise-mapping functionality but only returns the effective noise part of the noisy algorithm model. It does not require the Hamiltonian as input.

Overview

HQS Noise Mapper aims to identify the noisy algorithm model that can be effectively simulated on noisy hardware.

Input

In order to describe the dynamics of a quantum system the Trotterization method is applied to simulate the time evolution. This method may require the user to provide such parameters as Trotter step size or the number of Trotter steps.

Further required information is:

  • The Trotter step size, which is important for the correct re-scaling of the Lindblad terms of the calculated noisy algorithm model.
  • The original Hamiltonian (depending on the function you use).
  • The noisy quantum circuit (i.e., including noise gates) implementing a Trotter step of the time evolution of a Spin system for which we want to find the noisy algorithm model.
  • In the noisy quantum circuit, every portion needs to be wrapped in decomposition blocks to signal that the respective gate sequences within the blocks correspond to the application of a exponential that is parametrically small (i.e., comparable or smaller than the Trotter step size).
    • This is important information for the code to be able to commute noise through the circuit while staying within the error bars of the Trotter approximation.
    • Furthermore, the decomposition blocks contain all the information about swapping operations, and whether the qubit indices the noise acts on need to be remapped when commuting noise past the block.

Output

The output of our tool is then the sum of all generated noise terms, which corresponds to the Lindblad noise operator of the noisy algorithm model.

Conditions

Noise mapping works when the quantum algorithm under consideration is fundamentally of the Trotterization type, meaning that the original Hamiltonian can be written as a sum of local Hamiltonians \[ H = \sum_k H_k \] and the time propagation under each \(H_k\) is given by a well-defined sequence of native quantum gates.

The noisy algorithm model can be extracted from a quantum circuit that represents one Trotter step in a Trotterized time-propagation algorithm.

To be as general as possible, the noisy-algorithm extraction does not construct this quantum circuit that propagates a state for a virtual time. The noise mapper accepts circuits that have already been fully compiled for the target architecture and annotated with the necessary meta information.

Two forms of metadata annotation are required to apply noise mapping, as described in the following subsections:

  1. Marking the decomposition blocks, which are the parts of the circuit that correspond to implementing a partial time propagation under a \(H_k\)
  2. Information about the physical noise

1. Decomposition block annotation

Please note that HQS Noise Mapper is intended to be used in conjunction with the open source libraries qoqo and struqture by HQS Quantum Simulations GmbH.

The decomposition blocks are marked by inserting

  • a PragmaStartDecompositionBlock(qubits, reordering_dictionary) at the start of a decomposition block
  • a PragmaStopDecompositionBlock(qubits) at its end.

The qubits are in this case a list of qubits that are involved in the decomposition block. For example, when the decomposition block represents the time propagation under the partial Hamiltonian \(H_k = Z_2 Z_3\) of the interaction between two spins \(2\) and \(3\) and spins are mapped to qubits one to one, the involved qubits would be [2, 3].

The reordering_dictionary is used when a decomposition block not only implements a partial Hamiltonian time propagation but also reorders the qubits as is the case for SWAP networks. In the above example, if the decomposition block would also swap the definition of qubit \(2\) and \(3\) the reordering_dictionary would take the form,

reordering_dictionary = {2:3, 3:2}

Note: For the noisy algorithm model to be calculated, the decomposition blocks cannot overlap. A new decomposition block can only start once the previous decomposition block has been stopped. Also note that when inserting "book-keeping" operations in a circuit, such as SWAP operations, those operations also need to be enclosed in a decomposition block as they correspond to implementing the time propagation under an empty Hamiltonian \(H_k = 0\).

2. Noise information

The noise information is also directly annotated in the circuit. For generality, we do not assume a specific device-based noise model. The action of the physical noise on the quantum computer is represented by discrete noise operations that act at specific points in the circuit.

Please be reminded, that HQS Noise Mapper is intented to be used in conjunction with the open source libraries qoqo and struqture by HQS Quantum Simulations GmbH. For the annotation of noise in the input circuit the following qoqo operations can be used: PragmaDamping, PragmaDephasing, PragmaDepolarising and PragmaGeneralNoise, which all correspond to a Lindblad type master equation acting on a specific qubit for a finite gate_time. For more information see the qoqo documentation.

Noise mapping functions

The Noise Mapper provides two functions for noise mapping:

  • noisy_algorithm_model
  • noisy_algorithm_model_pure_noise

Function noisy_algorithm_model

The function noisy_algorithm_model returns the full noisy algorithm model including coherent terms. It takes as input the annotated circuit of one Trotter step, the original Hamiltonian and the Trotter timestep. The Trotter timestep represents the virtual time the system is propagated for during one Trotter step. The following code snippet briefly describes how the function is called.

from noise_mapper_py import noisy_algorithm_model

# Preprocessing noisy algorithm inputs
# ...

# Calling the noise mapper function
noisy_system = noisy_algorithm_model(
     circuit, #type Circuit
     hamiltonian, #type SpinHamiltonianSystem 
     trotter_timestep #type float
)

print(type(noisy_system)) # SpinLindbladOpenSystem

The function returns an object of type struqture_py.spins.SpinLindbladOpenSystem.

Note that the noisy_algorithm_model cannot check that the provided Hamiltonian corresponds to the time-propagation implemented by the circuit.

Function noisy_algorithm_model_pure_noise

The function noisy_algorithm_model_pure_noise also provides noise-mapping functionality but only returns the effective noise part of the noisy algorithm model. It does not require the Hamiltonian as input and it returns an object of type struqture_py.spins.SpinLindbladNoiseSystem.

from noise_mapper_py import noisy_algorithm_model_pure_noise

# Preprocessing noisy algorithm inputs
# ...

# Calling the noise mapper function
noise = noisy_algorithm_model_pure_noise(
     circuit, #type Circuit
     trotter_timestep #type float
)

print(type(noise)) # SpinLindbladNoiseSystem

Further examples

Readers can find detailed examples in the Examples.

Examples

In the following we give a minimal example for extracting the noisy algorithm model that implements one Trotter step for the time propagation under a Hamiltonian \[H=\sigma_x,\] where the time propagation is implemented by a sequence of three unitary gates: a Hadamard followed by a Z-rotation followed by another Hadamard. 

from noise_mapper_py import noisy_algorithm_model
from qoqo import Circuit
from qoqo import operations as ops
from struqture_py import spins

circuit = Circuit()
# To be able to construct the noisy alqorithm model
# the parts to the circuit simulation the
circuit += ops.PragmaStartDecompositionBlock([0], {})
circuit += ops.Hadamard(0)
circuit += ops.PragmaDamping(0, 1e-3, 1e-3)
circuit += ops.RotateZ(0, 0.01)
circuit += ops.PragmaDamping(0, 1e-3, 1e-3)
circuit += ops.Hadamard(0)
circuit += ops.PragmaDamping(0, 1e-3, 1e-3)
circuit += ops.PragmaStopDecompositionBlock([0])

system = spins.SpinHamiltonianSystem(1)
system.set(spins.PauliProduct().x(0), 2)
open_system = noisy_algorithm_model(circuit, system, 0.01)

print(open_system)