Introduction
The HQS Noise Mapper is a module that can be used in conjunction with other Quantum Libraries by HQS Quantum Simulations GmbH.
The HQS Noise Mapper provides a method for analyzing the effects of noise in quantum circuits, specifically those designed to simulate the time evolution of quantum spin systems through Trotterization. This method helps to understand the extent of noise effects and provides a good approximation to the actual dynamics of the noisy quantum circuit.
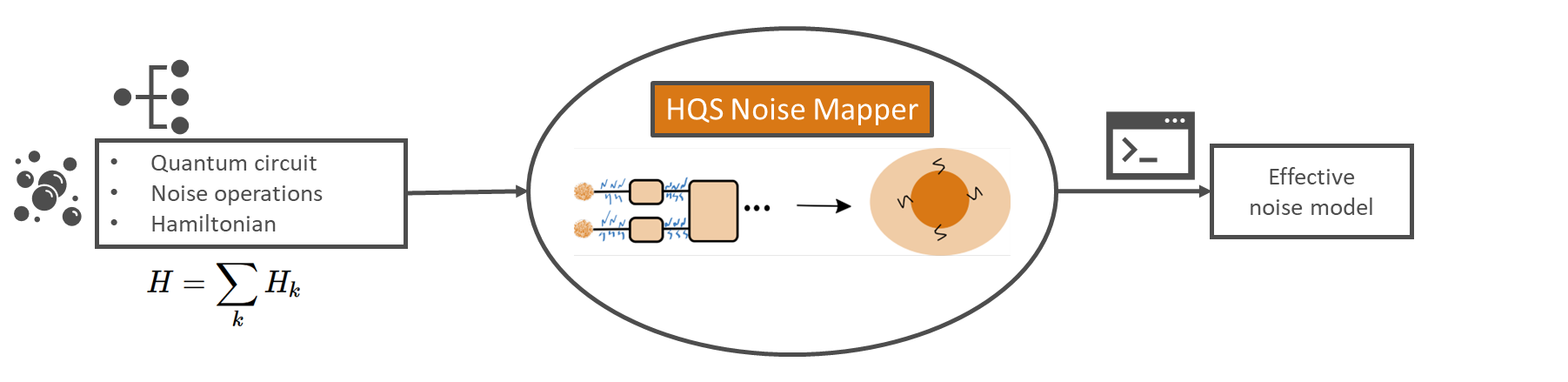
The primary goal of the HQS Noise Mapper is to calculate the noisy algorithm model that would effectively be correspond to running on a given noisy hardware device. Based on the input noisy quantum circuit corresponding to one time step, the output of the HQS Noise Mapper tool is the sum of all effective noise terms, corresponding to the Lindblad noise operator of the noisy algorithm model.
Applications
The time evolution of quantum systems is widely discussed as one of the most important applications of quantum computers, due to the exponential speedup these devices promise over conventional computers. However, today's universal quantum computing hardware is subject to errors (so-called “noise”), that have yet to be overcome. In order to enable useful, near-term quantum computing, it is crucial to understand the effects that noise can have on the results of a run performed on such a device.
The HQS Noise Mapper implements models to utilize the noise of the available devices to enable useful, near-term quantum computing. More specifically, it implements noise mapping, which is the construction of a static noisy algorithm model based on a quantum circuit and physical noise on a quantum computer. For further details on the scientific background of this method, please refer to the background section or our recent paper: arXiv:2210.11371.
Getting Started
The package can be installed with the following command:
hqstage install noise-mapper-py
The HQS Noise Mapper is a module that can be used in conjunction with other HQS Quantum Libraries by HQS Quantum Simulations GmbH.
Please note that the HQS Quantum Libraries are currently only supported on Linux and MacOS.
Users can find detailed examples in the Examples section.
Features
The HQS Noise mapper implements the Noisy Algorithm model. This is the static noise model, which determines the effective time propagation when a quantum algorithm for coherent time propagation under a Hamiltonian is run on a quantum computer with physical noise. In particular, the following functions are provided:
-
noisy_algorithm_model: Returns the full noisy algorithm model including the coherent terms. It takes as input the annotated circuit of one Trotter step, the original Hamiltonian, and the Trotter time step. -
noisy_algorithm_model_pure_noise: Provides noise-mapping functionality, but returns only the effective noise part of the noisy algorithm model. It does not require the Hamiltonian as input.
The noise mapper provides several interface functions for workflows and job run definitions. A detailed description can be found in the Python API documentation.
Conditions
- Noise mapping works when the quantum algorithm under consideration is fundamentally of the Trotterization type.
- The noisy algorithm model can be extracted from a quantum circuit representing one Trotter step.
- The noise mapper accepts circuits that have already been fully compiled for the target architecture and annotated with the necessary meta-information.
- Two forms of metadata annotation are required to apply noise mapping:
- Marking the decomposition blocks, i.e., the parts of the circuit that correspond to the implementation of a partial time propagation under a .
- Information about the physical noise.
- The noise mapping in the Noise Mapper is based on the assumption that the Trotter time step is short enough with respect to the Lindblad terms.
Please refer to the background section for more details.
Use Cases
The HQS Noise Mapper is designed to help users understand the effects of noise in quantum circuits.
-
Understand Device Noise: Helps users better understand the noise that the device actually experiences.
- This can be used, for example, for device characterization, i.e., to accurately simulate what is actually happening on the device in order to describe and characterize it, which helps in testing and improvement during the development lifecycle.
- Simulating noisy quantum computers can also be beneficial for benchmarking experimental results.
-
Time Evolution: Apply time evolution to the circuit with the effective noise model to get the time-evolved matrix and probabilities to study the dynamics of an open quantum system.
-
Algorithm Selection: Choose which algorithm to use when running a quantum program on a given device by analyzing which algorithm leads to less noise. The different algorithms can be found in the HQS Quantum Library
alqorithms. -
Analyzing Noise for NMR Simulations: Extract line width to predict how precise a noisy quantum computer can simulate NMR spectra.
Further Applications
Please note that the HQS Noise Mapper is intended to be used in conjunction with the open source libraries qoqo and struqture by HQS Quantum Simulations GmbH.
-
The output of the HQS Noise Mapper is a
struqtureobject calledPauliLindbladNoiseOperator, which represents the effective noise model. The output can be utilized with the quantum toolbox QuTiP to study the time evolution of relevant observables via the available struqture-qutip-interface provided by HQS Quantum Simulations GmbH. -
Additionally, the
PauliLindbladNoiseOperatorobject can be used to obtain an approximate time evolution beyond mean-field approximations, enabling the simulation of large systems.
Further Reading
The scientific background of this method has been published in a recent paper: arXiv:2210.11371.