Deciding which operators to discard

In order to decide which operators are "unimportant," Raqet makes a fundamental assumption about the physics of the system, which is that there exists a fundamental "length scale" beyond which correlations do not meaningfully spread. This assumption is plausible in local systems affected by noise, since the local interactions should generally result in a finite propagation speed for correlations, while in the presence of noise there is a time scale beyond which the system will decay to equilibrium, which is a state which will typically possess limited correlations. These two facts combined produce such an effective length scale. We can exploit this fact to eliminate degrees of freedom which extend over a region larger than this length scale.

In order to apply such a methodology to arbitrary quantum systems, we need a precise way to define a notion of "distance" between different "sites" in our quantum system. For now, we begin with the example of a simple lattice system, in which there exists an "obvious" notion of distance, and later we return to the more general case. An example of such a lattice system could be the one shown in the figure below. Each blue circle represents a quantum spin, with the distance between any two given positions being the shortest path through the links of the lattice. On such a lattice, we define the notion of the "diameter" of a collection of sites, which is the largest distance between any two sites in that collection. In the figure below, the dashed lines indicate collections of sites with a diameter of two.

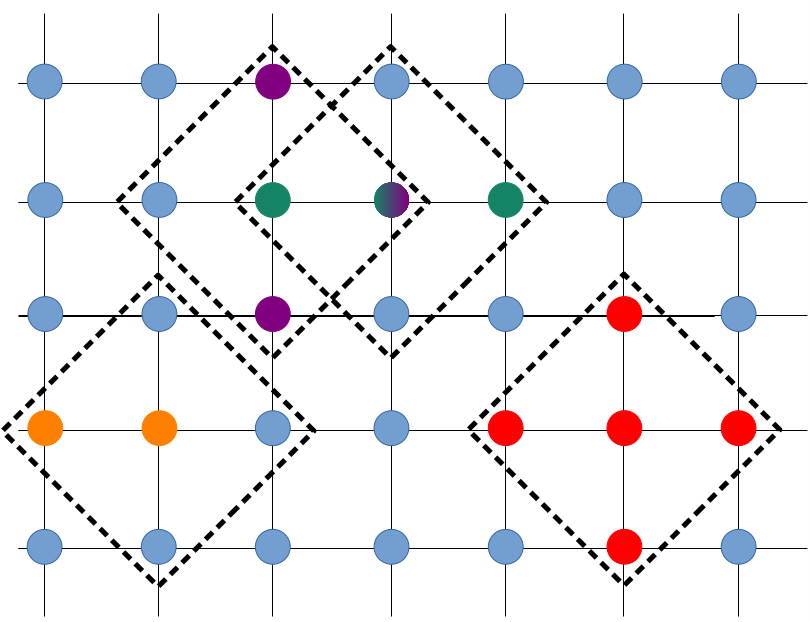
Any Pauli operator acting on such a system can be assigned a unique diameter. To see how, we consider the two sites colored in orange. The set containing only these two sites has a diameter of one, as this is (somewhat trivially) the largest distance between any two sites in this set. Any Pauli operator which involves these two sites can therefore be said to also have a diameter of one. For example, if these two sites were labeled as sites 1 and 2, then the operator \( \sigma_{1}^{z}\sigma_{2}^{z} \) would have a diameter of one. The other three collections of sites indicated in the figure, labeled with the colors red, purple, and green, all have diameters of two, and so any operators which involve those collections of sites would likewise have diameters equal to two.

With this definition, we can now state the fundamental approximation made by Raqet. To control the degree of approximation, a cut-off length scale is chosen. Any operator whose diameter is less than this cut-off scale is considered important, and is retained. All other operators are discarded.

Such an approximation is motivated by the notion of a Lieb-Robinson bound. In many local systems, there is a finite speed at which correlations can spread. If such a system is further subjected to noise, then this noise may ultimately drive the system into a steady state with limited correlations. The finite speed at which correlations spread, combined with the finite time over which noise will cause the system to undergo decoherence, leads to an effective distance scale over which correlations can never spread. Two sites which are further apart than such a distance scale can effectively never never develop correlations. If an operator contains two such sites, it would seem plausible that such an operator is "too big" to contribute important effects to the evolution of the system.

We emphasize here three important points about this condition.

First, we do not make any effort to "prove" why operators below a certain cut-off diameter should be important, nor do we attempt to derive what this cut-off should be. We simply take this assumption to be the defining approximation of Raqet. Whether or not this assumption is appropriate is ultimately determined by the performance of Raqet.

Second, we emphasize that the diameter is the key quantity when choosing which operators to keep, and not the number of sites involved in a Pauli operator. To clarify this point, we consider again the system indicated in the figure above, and imagine that we wish to control the degree of approximation by keeping all operators with a diameter of two or less. Any operator involving the sites in one of the colored sets (as well as many others) would be kept in this approximation. This includes, for example, any operators involving the sites colored in red, since even though there are five sites in this collection, the diameter of this set is still only two.

Third, our approximation does not correspond to making a partition of the system lattice. In the case that we choose to keep all operators with a diameter of two or less, we would keep (among others) operators which are defined on both the green and purple sets, even though these two sets overlap, and the combined region of overlap has a diameter of more than two.

More general notions of distance

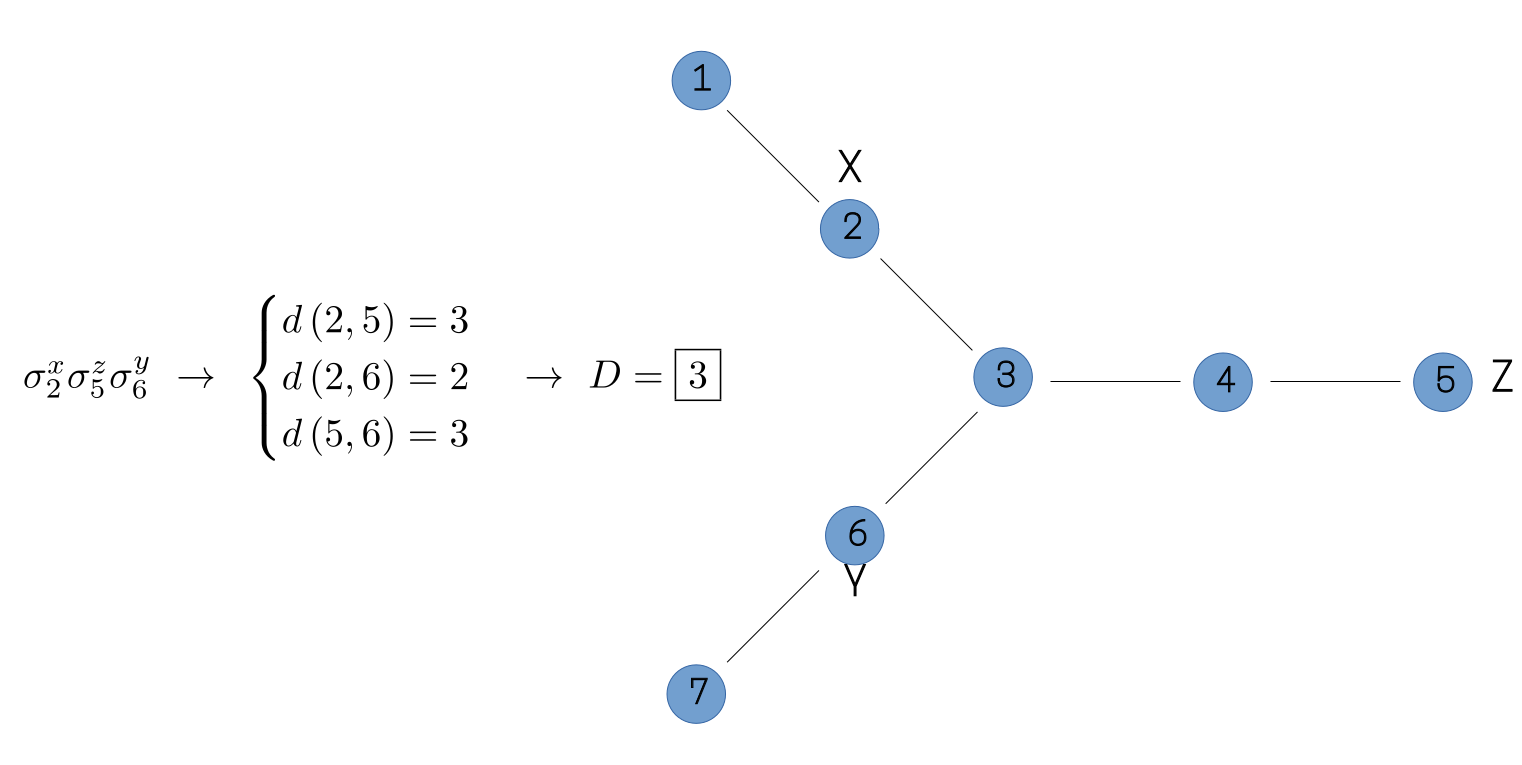
To apply these ideas to more general systems, we need to be able to generalize the concept of a distance function between two sites, beyond the case of simple lattice systems. In principle, this distance function can be any function which satisfies the mathematical definition of a metric. In practice, however, the distance function should ideally reflect something about the physics of the system. To see one example of how we might accomplish this, we consider the example system in the figure below. Such a system might represent a toy model of a molecule to be studied in an NMR experiment, with the sites corresponding to the nuclear spins of its constituent Hydrogen atoms. For such a system, we may wish to compute the diameter of, for example, the operator \( \sigma_{2}^{x}\sigma_{5}^{z}\sigma_{6}^{y} \). If we again consider the distance between any two sites to be the number of lattice links which must be traversed in order to travel from one site to the other, then we would assign a diameter of three to this operator, as shown in the figure.

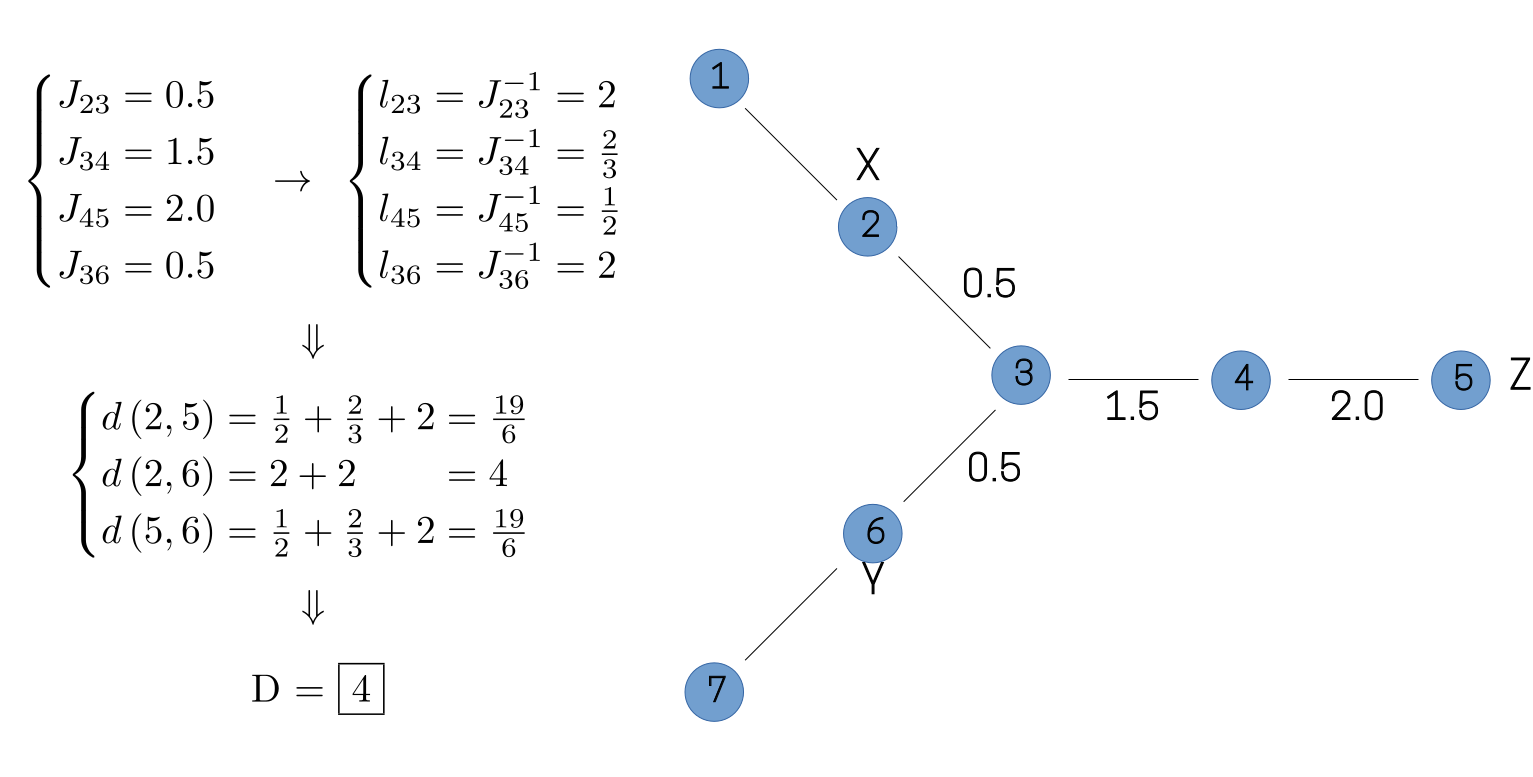
In many physical systems, however, the couplings between individual sites in a system are not uniform. It would therefore seem natural to account for this lack of uniformity when determining the distance between different sites. One way to accomplish this is shown in the figure below, in which the connections between sites have been labeled with hypothetical Hamiltonian couplings. If we imagine the "length" of these individual connections to be inversely proportional to the corresponding Hamiltonian couplings, then the distance traveled between any two spins will now differ from the naive calculation, leading to a diameter of four for this operator, rather than three.

Of course, in most cases of physical interest, the Hamiltonian couplings will result in multiple possible paths between any two sites. In such a situation, there are several available options for defining a distance function. One option is to choose simply the shortest possible path between any two sites, while a somewhat more involved metric imagines the couplings to represent a sort of resistance network between sites, with the distance between any two sites now corresponding to the effective resistance between them. The choice of distance function will result in slightly different values for the diameter of our operator, as illustrated in the figure below.

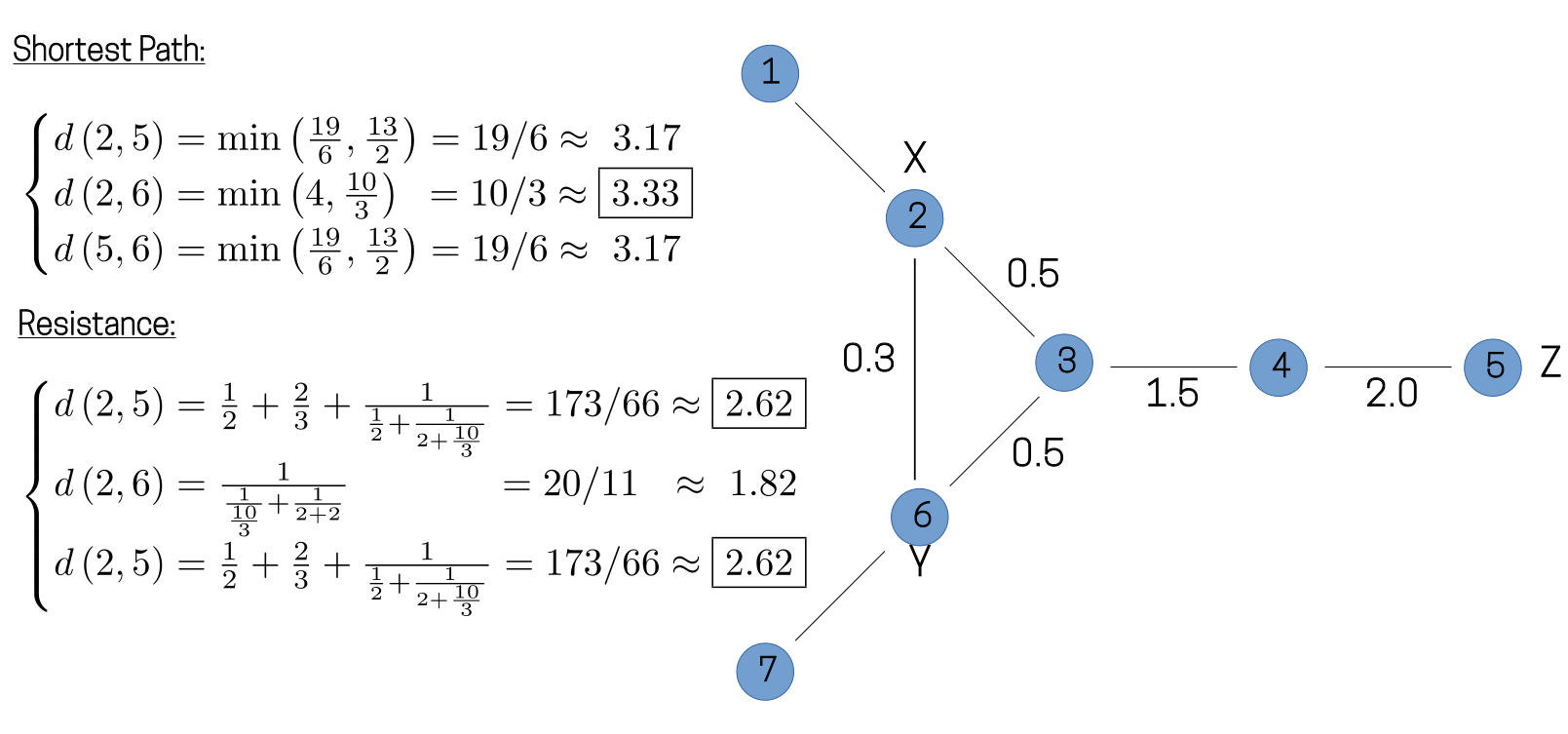
While we could continue to refine our notion of distance for this example system, in practice, we have found reasonably good results by making use of the ideas we have developed so far. In some sense, the "best" possible distance metric for any given system should measure the amount of time it takes for correlations to develop between two sites, since the fact that correlations spread throughout the system at a finite speed is the underlying physical motivation for the method. Of course, knowledge of this type of information would generally require a solution to the dynamics, which is precisely what we wish to find using Raqet. Thus, some amount of physical intuition will always be necessary when postulating a notion of distance.