Introduction
HQS Qolossal is a Python package that provides access to an efficient tight-binding solver with computational scaling linear in system size. The approach, based on the expansion of quantities of interest in Chebyshev polynomials, allows for efficient simulations of systems with up to billions of sites.
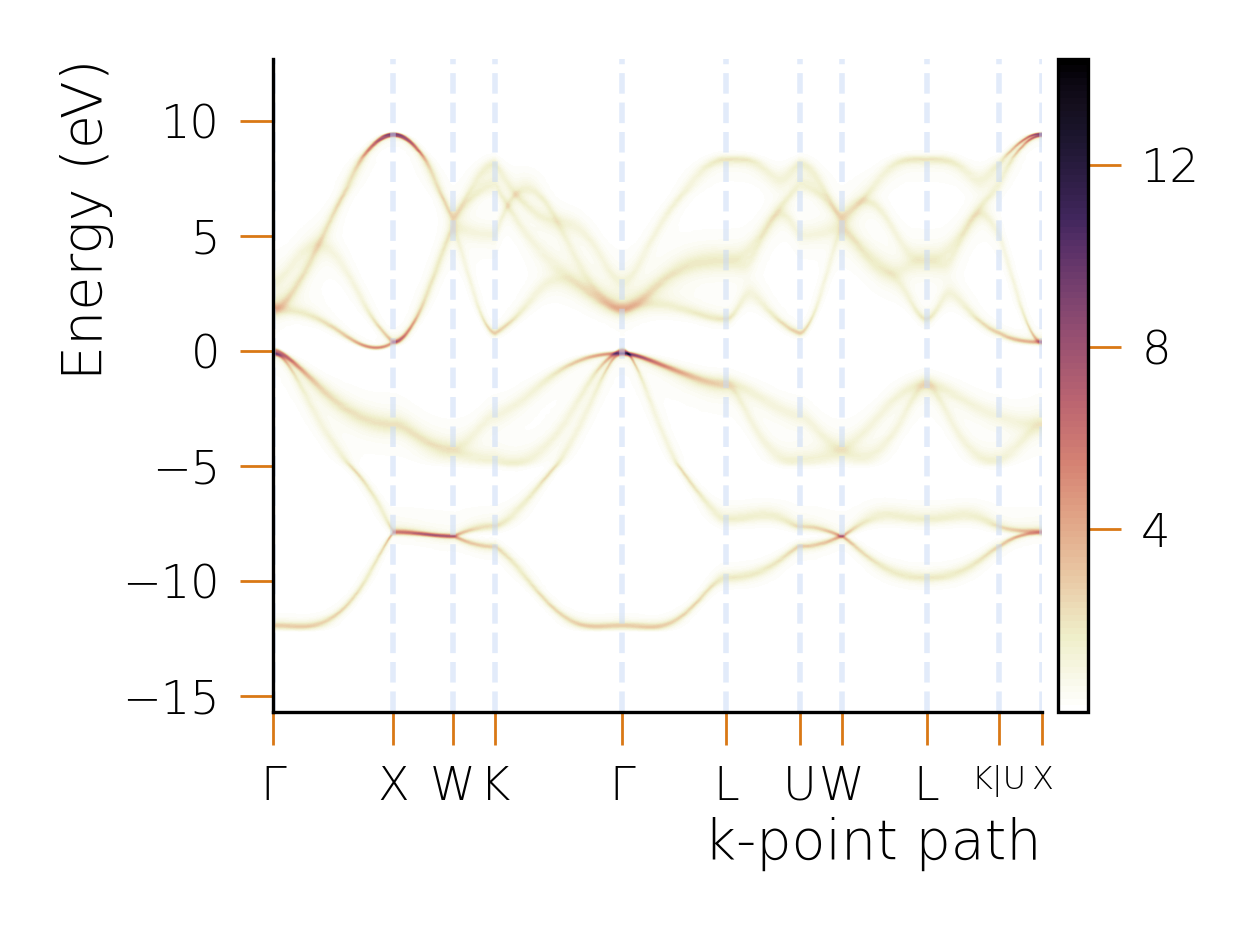
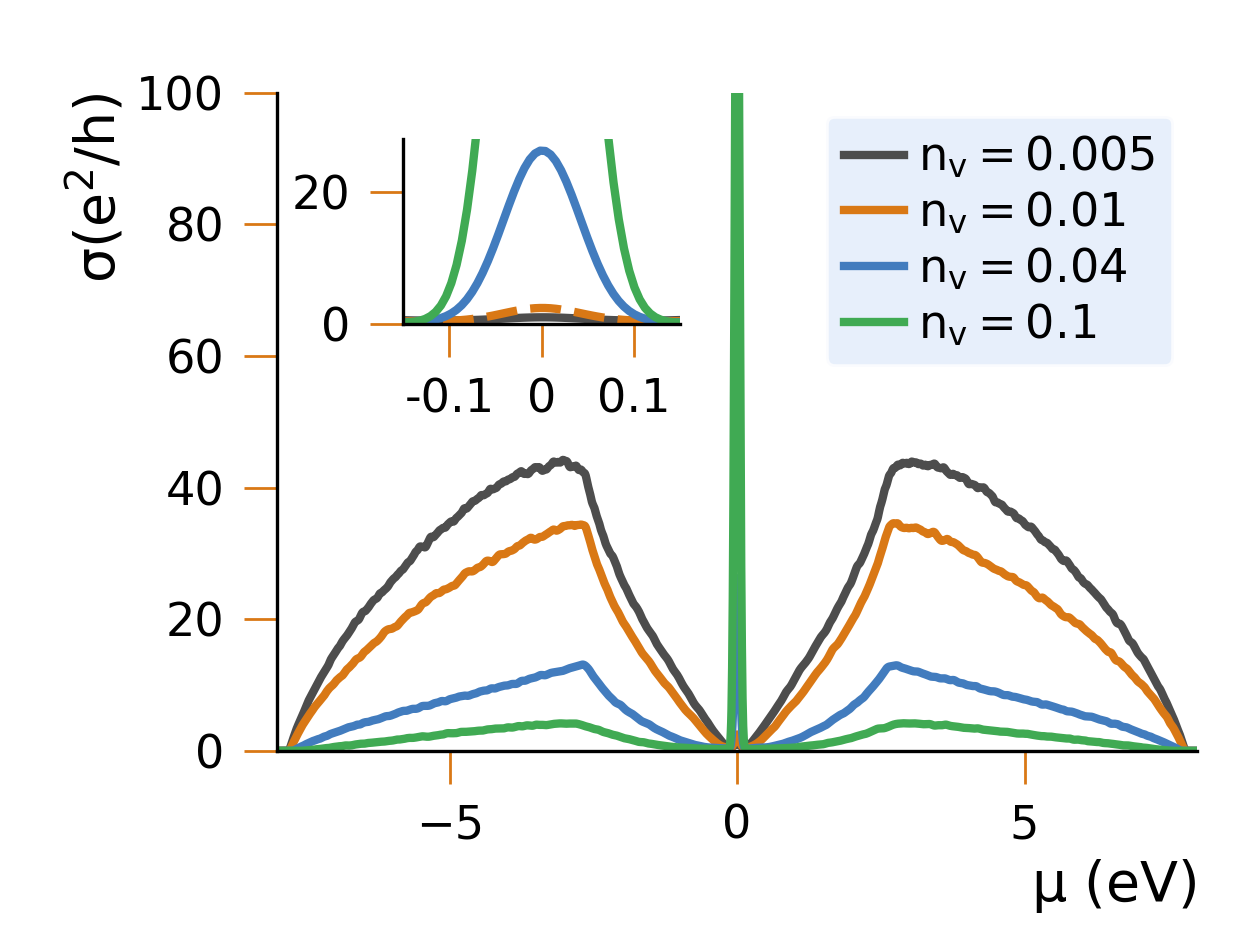
Applications
To study the material properties of devices, it is sometimes necessary to include millions of sites in a materials science simulation - having an efficient way to handle these systems is therefore paramount. By scaling to millions/billions of sites, HQS Qolossal can capture phenomena at the device scale, making it possible to analyze, for example, semiconductor heterostructures, or the effects of structural defects in materials, or the topological effects in 2D materials.
Getting started
To install HQS Qolossal simply run
hqstage install qolossal
after having installed HQStage. Once installed, you can proceed to set up and run your calculations. More information about this can be found in the examples section.
Features
The following quantities can be calculated with HQS Qolossal:
- Density of states
- Trace of the resolvent
- Green's function
- Electrical conductivity
- Expectation value of user-defined operators
- Static linear response of user-defined operators to user-defined perturbations (e.g. susceptibilities)
- Spectral function
- Chemical potential
- Optical electrical conductivity
- Carrier density for semiconductors
- Electron mobility for semiconductors
- Electron diffusion coefficient for semiconductors
- Permittivity
- Normal incidence reflectivity
- Absorption coefficient
For further information refer to the API documentation.
Theory
Linear scaling method
The linear scaling method we use is based on the expansion of the quantities of interest we want to study in terms of Chebyshev polynomials. These polynomials have been routinely employed in chemistry and physics and exhibit greater accuracy compared to other sets of orthogonal polynomials. In what follows, we give a brief introduction to the topic. For more details, see this reference.
The expansion of a function in terms of Chebyshev polynomials of the first kind reads where is the n-th Chebyshev polynomial of the first kind and is its corresponding moment. The Chebyshev polynomials benefit from the following advantageous recursion relation
Although the above-mentioned expansion is correct and efficient, it can be problematic when evaluating the moments due to the form of the denominator. A considerable simplification can be introduced by working with the modified orthogonal functions and the corresponding dot product:
Rewriting the expansion in this modified framework yields
which, as we will see later, allows for an efficient recursive calculation of the moments.
For our purposes, the quantities we aim to represent using the Chebyshev polynomials basis are functions of the Hamiltonian rather than of a simple independent variable. Before expressing these functions as a Chebyshev expansion, it is important to ensure that the spectrum of the Hamiltonian lies within the interval , as the expansion is only defined there. If needed, the Hamiltonian should be rescaled by
where is the center of the original spectrum and is its full width. For simplicity, in what follows, we omit the ~ sign on the Hamiltonian; however, we will always refer to the scaled Hamiltonian. The results obtained will need to be appropriately scaled back to fit the original spectrum, hence the Hamiltonian 1. The quantities of interest, which are functions of the (rescaled) Hamiltonian, can be expressed as a Chebyshev series by observing
where the set consists of the single-particle eigenfunctions of the Hamiltonian with eigenvalues . As an example, let us explicitly write the expansion of the density of states, i.e.
The operator to be traced is, as we just pointed out, a function of the Hamiltonian. By inserting the resolution of the identity and using the manipulations shown above, we obtain
The expansion of the density of states in terms of Chebyshev moments is then
This expression, though exact, is not particularly convenient, as it requires knowledge of all single-particle eigenfunctions . This would defeat the purpose of any other calculation, since knowledge of these eigenstates and their corresponding eigenvalues defines any property of the system 2. Nonetheless, the form presented above is used in our code to evaluate specific matrix elements of functions of the Hamiltonian - e.g., Green’s function matrix elements in the site basis, for which only a single evaluation is necessary. Fortunately, the calculation of the trace can be approximated in an efficient and accurate way through a stochastic evaluation 3 4. In this approach, the trace of a general single-particle operator is approximated as
where the set of consists of random states constructed from independent and identically distributed random coefficients with zero mean. The vectors are normalized to 1, which ensures that they can indeed be considered states for the purpose of our calculations. This means, however, that when evaluating quantities such as the density of states, the average over the random states will be normalized to 1 rather than to the number of particles. In terms of accuracy, it has been shown 5 that the error of the approximation is proportional to , where N is the system size and R is the number of random vectors employed in the stochastic evaluation. This works in our favor, as the accuracy increases with the system size - so much so that, for a system with a billion sites, averaging over only a few states is sufficient for most purposes 6: in this case .
Kubo formula for the conductivity
For the analysis of linear response, we use a method based on the Kubo formula. In this context, we focus on the case of responses to electrical signals. According to the Kubo formula, the response of an operator to a zero-frequency (DC) perturbation is givem by
where is the volume of the system, is the intrinsic lifetime, is the equilibrium density, is the DC perturbation, and is the current operator. If the general operator , we have
where the volume has been ‘absorbed’ into the current, and we are considering the spatially averaged quantity. According to Ohm’s law, the quantity in the brackets in the equation above represents the DC conductivity . This formula simplifies considerably in the non-interacting case. Following the steps detailed in 7, we can rewrite the above equation as
where the Fermi occupation function and the denominator of the fraction come from the density matrix. Additionally, the following property has been used
where are the single particle eigenfunction of the Hamiltonian with energy . Rewriting this equation in terms of Green’s functions, one obtains
where are the retarded and advanced Green’s functions. This formula is referred to as the Kubo-Bastin formula and is equivalent to the Kubo formula for non-interacting systems.
If we focus on the conductivity, i.e. , where q is the carrier charge and is the velocity operator, then with some simple manipulations, we arrive at
where we make use of . Integrating the last equation by parts leads to
where the derivative of the Fermi function acts as a window, selecting the energies around the chemical potential that contribute to the dissipative conductivity, as expected. The zero-temperature limit of the above equation is the so-called Kubo-Greenwood formula
where we make use of the identity . For simplicity, the direction of the velocity operators has been omitted, but for calculating any element of the conductivity tensor, one simply needs to use the velocity operators in the corresponding directions, i.e.
This formula can then be expanded in terms of Chebyshev polynomials by transforming the delta functions back into Green’s functions and evaluating the corresponding moments for the stochastic samples, as shown in 7, with the only difference being the normalization of the random states and, consequently, the volume prefactor 8.
Velocity operator
As shown in the previous sections, to compute the conductivity of the
system, we need the velocity operator. In this section, we demonstrate how this
is handled when the system is initialized via the Lattice Validator input.
The velocity operator can be computed using Heisenberg’s equation of motion,
, where is the
position operator. While this is, in principle, a simple operation
requiring two matrix-matrix multiplications and an addition, it becomes
ill-defined for generic boundary conditions other than hard-wall. In
fact, the position operator cannot be defined for periodic systems, and
the above-mentioned formula fails. This problem, however, can be circumvented by
using the 'distance' information provided by the various bonds that make
up the Hamiltonian. Specifically, the translation vector associated with each bond will
give us information about the real-space displacement between the two unit cells it
connects, i.e. all the spatial information we need to compute the commutator .
The periodic boundary conditions are then automatically handled
when implementing the recipe given by the translation associated with
each bond to construct the full operator, much like the construction of
the Hamiltonian. Note that it is not important where spatial origin is
set, as it would simply introduce a contribution proportional to
the identity in the position operator, which does not contribute to the
value of the commutator. As an example, let us consider the case of an
unevenly connected chain, as shown in the following figure:

This system has the following Hamiltonian (on the lattice)
Considering a unit cell made of two different sites, this Hamiltonian can equivalently be represented by the following bond information
where the vector represents the translation in terms of unit cells associated with the bond (hence is the bond within the unit cell), and are matrices spanning the different sites of the unit cell, indicating the connections within the different sites and their corresponding strengths. Since the Hamiltonian is the sum of the contributions from the two bonds, we can sum the velocity contributions associated with each bond. In this system only the x-component of the velocity operator will be non-zero. For the trivial translation associated with the bond , the commutator can be directly evaluated, where is the first bond Hamiltonian from the previous equation and the matrix is simply the position operator within the unit cell. For the second bond, a similar approach can be used, but care must be taken with the position operator. Let us now consider the subspace made of the original unit cell and the cell reached by the translation , i.e. the displacement associated with the bond
The position operator in the x-direction, in the site basis within this subspace 9, reads:
where is the null matrix, is the position in the x-direction of the site and is the displacement in the x-direction corresponding to the lattice vector. The matrices and are the position operators in the original unit cell and the displaced one, respectively. Note that, in general, the displacement vector is
where is the translation associated with the bond for the i-th lattice vector . Our example is the trivial case of a translation by a single lattice vector of magnitude one. In the same subspace, the Hamiltonian contribution of the (directional) bond is
The position of non-zero block is determined by the directionality of the bond definition: if the translation were , i.e. hopping to the left, the non-zero block would be the lower left one. In terms of the block representation, it is straightforward to evaluate the commutator
where the superscript denotes that the contribution to the corresponding quantities comes from the bond . Since the block structure of the resulting contribution to the velocity operator is the same as the bond, one can construct the velocity associated with each bond as , and distribute these across the whole system in the same way that the Hamiltonian is constructed. The storage strategy will be the same as well, simply keeping track of the (intra-)inter-cell velocity contributions and the associated translations. In this sense, the boundary conditions do not represent a problem from this perspective, because the correct behavior of the velocity operator is imposed by means of the distribution functions, i.e. how the sub-blocks are repeated in the matrix corresponding to the whole system.
Transport properties
HQS Qolossal offers the possibility of calculating carrier mobility and diffusion coefficient. These are quantities derived from the DC conductivity and the density of states.
Carrier mobility
with e electron charge, the electron (hole) density, the DC conductivity and, finally, the mobility.
Diffusion coefficient with the DC conductivity, the density of states and the diffusion coefficient. All quantities refer to their values at the specified chemical potential .
Optical properties
The optical electrical conductivity is computed via the Chebyshev expansion of the well-known Kubo-Bastin formula10
with the fermi function, the velocity operator and the components of the Greens function. This is expanded into Chebyshev polynomials the same way as for the DC conductivity. All other optical properties are derived from the optical conductivity. Below all definitions.
Permittivity
Reflectivity Absorption coefficient
Bibliography
-
This means that any prefactor coming from the rescaling of the Hamiltonian has to be included. For example, the expansion of the density of states will be presented later in the text. The delta function contained in its definition will yield . The factor will have to be included in the final rescaling to obtain the correct result. ↩
-
Aside from representing a computational effort which scales like the cubic power (or square, if the Hamiltonian is sparse) of the system's size, since it is the diagonalization of the whole Hamiltonian. ↩
-
Drabold, David A., and Otto F. Sankey. 1993. “Maximum Entropy Approach for Linear Scaling in the Electronic Structure Problem.” Phys. Rev. Lett. 70 (June): 3631–34. https://doi.org/10.1103/PhysRevLett.70.3631. ↩
-
Silver, R. N., and H. Röder. 1994. “DENSITIES OF STATES OF MEGA-DIMENSIONAL HAMILTONIAN MATRICES.” International Journal of Modern Physics C 05 (04): 735–53. https://doi.org/10.1142/S0129183194000842. ↩
-
Weiße, Alexander, Gerhard Wellein, Andreas Alvermann, and Holger Fehske. 2006. “The Kernel Polynomial Method.” Rev. Mod. Phys. 78 (March): 275–306. https://doi.org/10.1103/RevModPhys.78.275. ↩
-
The appropriate number of random states to average over also depends on the order of the expansion: the higher the number of moments, the lower the frequency resolution of the expansion, hence the larger the sampling pool must become. ↩
-
Fan, Zheyong, José H. Garcia, Aron W. Cummings, Jose Eduardo Barrios-Vargas, Michel Panhans, Ari Harju, Frank Ortmann, and Stephan Roche. 2021. “Linear Scaling Quantum Transport Methodologies.” Physics Reports 903: 1–69. https://doi.org/https://doi.org/10.1016/j.physrep.2020.12.001. ↩ ↩2
-
The corresponding volume will be the volume of the unit cell instead of the total volume. ↩
-
Note that, in this case, the subspace mentioned is equivalent to the whole system, but in any case with more than two unit cells, this will not be the case. ↩
-
Jose H. Garcı́a, Lucian Covaci, and Tatiana G. Rappoport. 2015. "Real-space calculation of the conductivity tensor for disordered topological matter". Phys. Rev. Lett., 114, p. 116602. https://doi.org/10.1103/PhysRevLett.114.116602. ↩
Examples
In this section we will showcase the basic usage of HQS Qolossal. For more advanced examples,
please download the example notebooks via HQStage.
To compute system properties with HQS Qolossal, we simply need to initialize a Hamiltonian object.
Once this has been correctly set up, one can invoke all available methods that directly compute the corresponding physical quantities — no extra setup is required. HQS Qolossal offers several Hamiltonian implementations for ease of use. In the following examples, we provide more details on how to handle them.
Take a look at these pages for further details
Hamiltonian set up
HQS Qolossal supports different ways of defining Hamiltonians: via abstract definition, via directly providing the Hamiltonian in matrix form or as a linear operator. Additionally, you can add disorder to your systems.
Hamiltonian as a structured input
Setting up a Hamiltonian can be done via structured input using the Lattice Builder.
Please refer to its documentation
for more information. In short, to define a lattice system, you need to specify which atoms/sites
make up the unit cell, which bonds connect them, and other important information regarding the structure.
The corresponding input dictionary can be directly handed to HQS Qolossal for initialization, for example:
from qolossal import HamiltonianSparse
unitcell = {
'atoms': [
{'id': 0, 'name': 'A', 'position': [0.0, 0.0, 0.0], 'e0': 0.0}
],
'lattice_vectors': [[1.0, 0.0, 0.0]],
'bonds': [
{'id_from': 0, 'id_to': 0, 'translation': [1, 0, 0], 't': -1},
],
}
system = {
'system_size': [1000, 1, 1],
'site_type': 'spinless',
'system_boundary_condition': ['PBC', 'HW', 'HW']
}
lb_input = {
'unitcell': unitcell,
'system': system
}
H = HamiltonianSparse(lb_input)
The script above initializes a 1D chain of length 1000 as a sparse Hamiltonian.
Hamiltonian as a matrix
Setting up a Hamiltonian in its matrix form is as simple as expected: we simply need to initialize the corresponding Hamiltonian class with it. Let's make the example of a 1D chain, where the non-zero entries in the Hamiltonian are just the two off-diagonals with value
import numpy as np
from scipy.sparse import diags
from qolossal import HamiltonianSparseDirect
# parameters
t = 1 # hopping amplitude
dimension = 10 # dimension of the chain
lattice_vector_length = 0.5 # in Angstroms
# initialize the hamiltonian matrix.
# NOTE: we use the csr format as this is what qolossal uses
diagonals = -t * np.ones(dimension)
Hamiltonian_matrix = diags(
diagonals=[diagonals, diagonals],
offsets=[1, -1],
shape=(dimension, dimension),
format='csr'
)
# initialize HamiltonianSparseDirect.
H = HamiltonianSparseDirect(
H = Hamiltonian_matrix,
total_volume = dimension * lattice_vector_length
)
This will initialize our Hamiltonian object and we will be able to start computing the systems properties. The above code will result in a RuntimeWarning: since we have not provided the velocity operators, the calculation of quantities that require them — such as the DC conductivity — will not work. To do so, we follow the same rationale
sites_position = np.arange(dimension) * lattice_vector_length
position_operator = diags(
[sites_position],
offsets=[0],
shape=(dimension, dimension),
format='csr'
)
# compute the velocity as V_x=i [H, r_x] (hbar=1)
velocity_x = 1.j * (
Hamiltonian_matrix @ position_operator - position_operator @ Hamiltonian_matrix
)
# the velocity matrices for the y and z directions are just zeros.
velocity_y = velocity_z = diags(
np.zeros(dimension),
shape=(dimension, dimension),
format='csr'
)
# initialize HamiltonianSparseDirect.
H = HamiltonianSparseDirect(
H = Hamiltonian_matrix,
total_volume = dimension * lattice_vector_length,
velocity_times_hbar_matrices=[velocity_x, velocity_y, velocity_z]
)
Now we can proceed to compute velocity-dependent quantities as well.
Hamiltonian as a linear operator
To initialize the Hamiltonian with a linear operator we proceed exactly like for the matrix version.
import numpy as np
from scipy.sparse import diags
from qolossal import HamiltonianLinearOperator
# parameters
t = 1 # hopping amplitude
dimension = 10 # dimension of the chain
lattice_vector_length = 0.5 # in Angstroms
# initialize the hamiltonian matrix.
# NOTE: we use the csr format as this is what qolossal uses
diagonals = -t * np.ones(dimension)
Hamiltonian_matrix = diags(
diagonals=[diagonals, diagonals],
offsets=[1, -1],
shape=(dimension, dimension),
format='csr'
)
# we define the linear operator starting from the matrix for the example, but this can be
# done however one likes
def linear_operator(v: np.ndarray, out: np.ndarray) -> np.ndarray:
"""Apply Hamiltonian to vector.
Args:
v (np.ndarray): input.
out (np.ndarray): preallocated output.
Returns:
np.ndarray: H @ v
"""
# syntax used to make sure that the result is written in the already allocated space of "out"
out[:] = Hamiltonian_matrix @ v
return out
H = HamiltonianLinearOperator(
linear_operator,
dim=dimension,
dtype=float,
total_volume=dimension * lattice_vector_length
)
For the velocity we proceed in exactly the same way, ensuring the linear operators have the same signature as the Hamiltonian linear operator.
Disorder
HQS Qolossal can also add disorder to the system. Currently only local disorder is implemented:
in this case a random potential is applied to the different sites. To add local disorder to a
system, we can simply specify its properties during the Hamiltonian initialization:
from qolossal import HamiltonianSparseDirect
# ... initialization of all relevant arguments
H = HamiltonianSparseDirect(
H = Hamiltonian_matrix,
total_volume = dimension * lattice_vector_length,
disDict={"type": "onsite", "distr": "uniform", "sigma": 0.1, "avg": 0}
)
where the disorder dictionary specifies the type of disorder (currently only "onsite"), the distribution type
of the random potential (allowed: uniform, gaussian, laplace), as well as the average value
and standard deviation of the random potential.
Calculations
Once the Hamiltonian has been set up, we can call any method offered by HQS Qolossal to compute
physical quantities of the defined system. Let's look at the example of the density of states (DOS)
for the 1D chain we defined in the previous sections:
# ... initialize Hamiltonian
# scale the Hamiltonian to allow for the Chebyshev expansion to work
H.scaleH()
# calculate the density of states
dos, w = H.getDOS(
NSamples=20,
Order=200,
NOmegas=2000
)
plt.plot(w, dos)
plt.xlabel("Energy (eV)")
plt.ylabel("DOS")
plt.show()
In this case, the arguments passed to the function control the number of random samples used for the DOS calculation, the order of the expansion, and the number of frequencies at which the DOS is calculated. The above code will produce this following result:
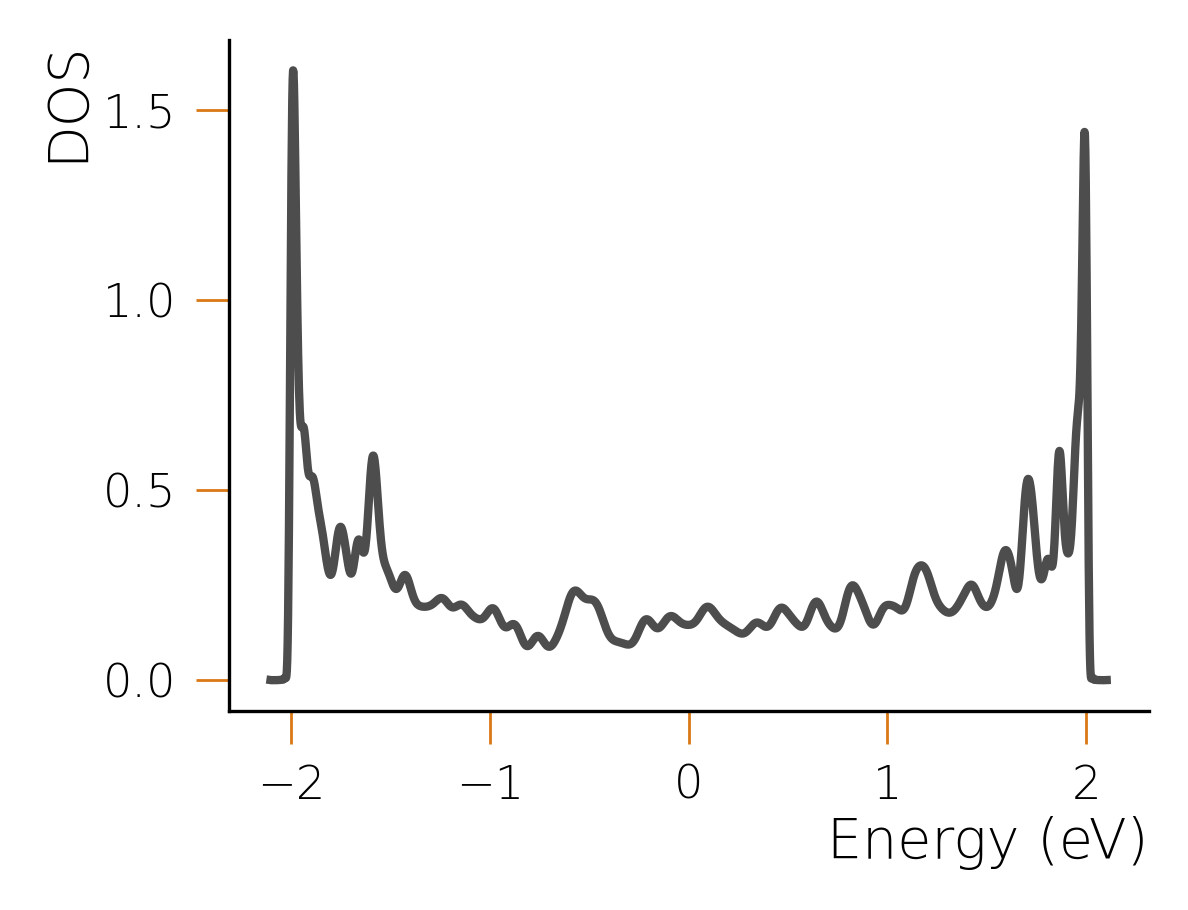
The wiggles in the result depend on the stochastic nature of the calculation and can be converged
to the correct result by adjusting the convergence parameters. Larger systems (for which HQS Qolossal
is designed) require fewer random samples and, counterintuitively, converge faster to much smoother
results thanks to self-averaging properties. In fact, using the same setup but with a chain of
size 20000, an order of the expansion of 1200 and 200 samples for the stochastic evaluation, we
obtain the following result:
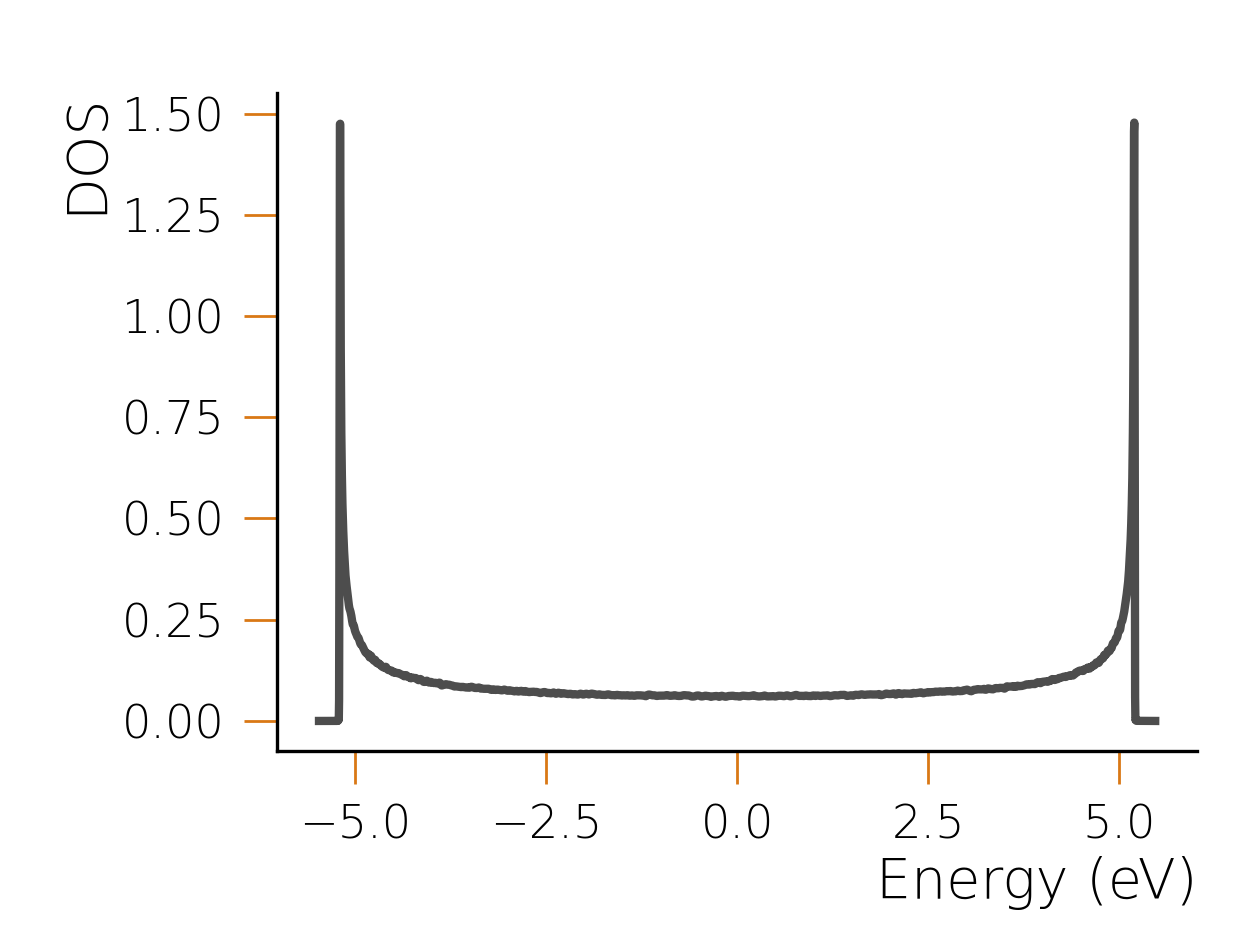
Units
This page serves as a reference for the input and output units in Qolossal. The symbol in the following sections represents the dimensionality of the system.
Input parameters
| Quantity | Unit |
|---|---|
| Energy | electronvolt () |
| Length | Angstrom () |
| Temperature | Kelvin () |
Output Quantities
| Quantity | Unit |
|---|---|
| DOS | |
| Conductivity | |
| Chemical potential | |
| Carrier Density | |
| Mobility | |
| Diffusion coefficient | |
| Permittivity | unitless |
| Reflectivity | unitless |
| Absorption Coefficient |