Examples
In this page, we use the system-bath tool to solve dynamics of some simple system-bath problems and study the quality of the corresponding quantum simulation. Notebooks with the examples are available in the examples repository of the HQS Noise App.
Spin coupled to broad bosonic mode
We first look at a system coupled to one bosonic mode, described by the Hamiltonian
\[ H = \frac{\Delta}{2}\sigma_z + \frac{1}{2}\sigma_x(g a + g^* a^\dagger) + \omega_0 a^\dagger a \nobreakspace . \]
The coupling to the bosonic mode is ultrastrong, \(g\sim\omega_0\). This makes the representation of the bath using spins challenging, but not impossible. Below, we show how the bosonic bath can be represented by a spin bath. We assume that the system qubit is noiseless, the bath qubit noise is due to decay and dephasing, and that the noise is "on" constantly.
For each Trotter step, we need to correctly scale the phases of the digitally implemented small-angle gates, so that the physical broadening matches with the model broadening. For example, we need to fix the phase of the system-bath coupling so that:
\[ \begin{align} &\varphi_g \equiv g_\textrm{simulation}\tau_\textrm{simulation} = \frac{g_\textrm{fit}}{\gamma_\textrm{fit}} {\cal N} \\ & {\cal N} = D \gamma_\textrm{physical}\tau_\textrm{physical} \nobreakspace , \end{align} \]
where \(D\) is the circuit depth. It accounts for the accumulation of the noise. The parameter \({\cal N}\) is then a measure of total infidelity of one Trotter step.
To demonstrate the possibility to also include bath-qubit dephasing to effective broadening, we consider the case where the boson-mode-broadening \(\kappa\) is reproduced by an equal contribution from qubit decay \(\gamma\) and dephasing \(\Gamma\),
\[ \begin{align} \kappa &= \gamma + 2\Gamma \\ \gamma &= 2\Gamma = \frac{\kappa}{2} , . \end{align} \]
Furthermore, we consider the parameters:
\[ \begin{align} g &= 1 \\ \omega &= 1 \\ \Delta &= 0.9 \\ \kappa &= 0.5 \nobreakspace . \end{align} \]
We also use \({\cal N} = 0.02\), which is a relatively high value, but still does not lead to a noticeable Trotter error. The larger this parameter is, the more Trotter error the quantum simulation will have.
Below, we show a comparison between the exact spin-boson model and the quantum simulation for the (native) variable MS-decomposition, where the bath is described either by 1 spin or 6 identical spins. The simulation starts from the system-spin being in the +1 eigenstate of operator \(\sigma^x_\textrm{system}\) and the bath being in its groundstate. We track the time evolution of \(\langle \sigma^x_\textrm{system}(t) \rangle\).
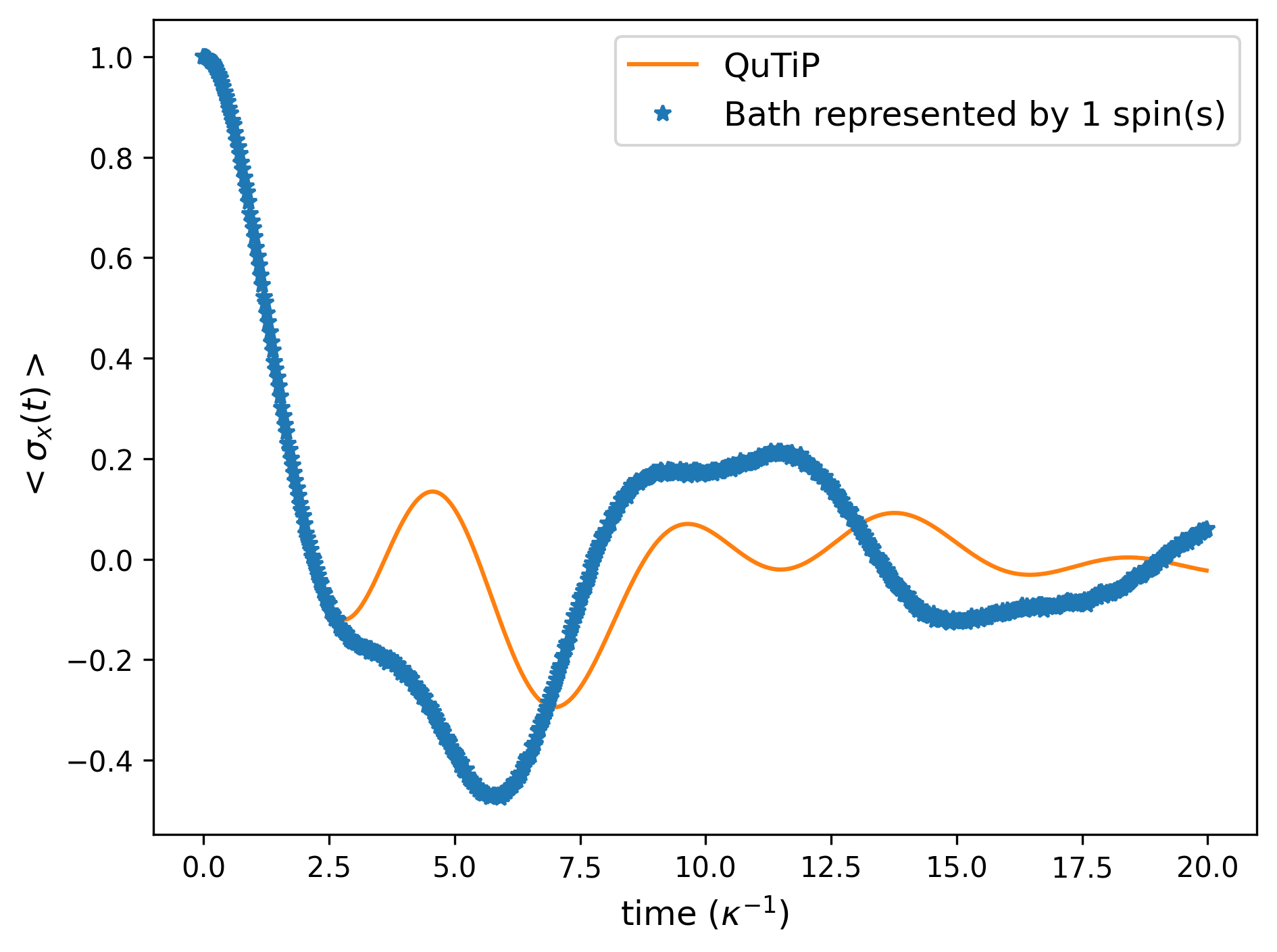
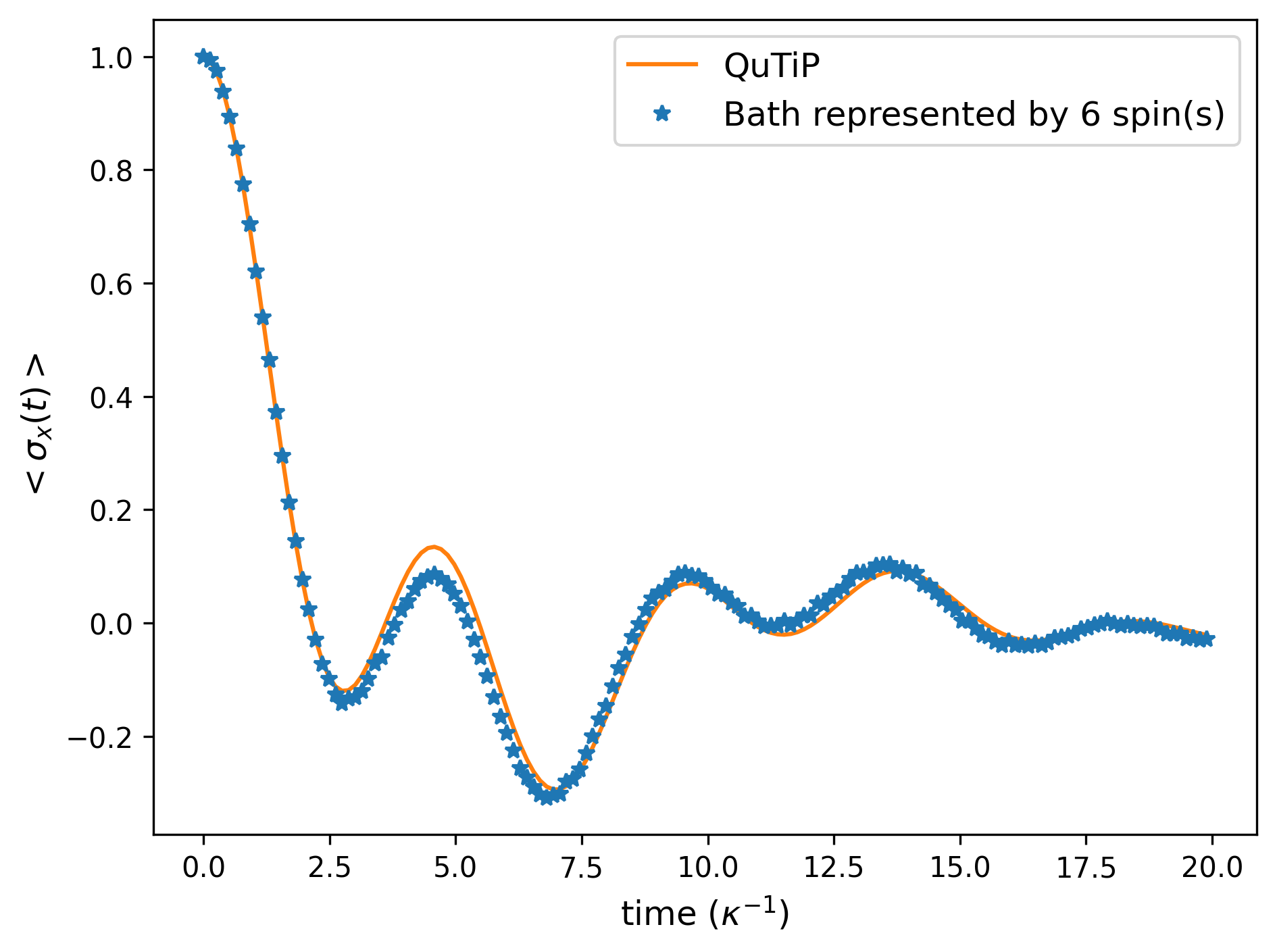
We see that the quantum simulation with 1 spin gives incorrect dynamics, whereas for 6 spins the dynamics are almost identical to the correct result. The remaining difference is due to the finite number of bath spins. The trotter error is here negligible.
In the next figure, we study the same system, but run the simulation with a non-native gate decomposition (CNOT). Here, we use the bath qubits as control qubits when performing CNOT gates. The simulation is performed for 8 bath qubits.
We again find a very small difference between the ideal spin-spin model and the quantum simulation, though now with a marginally larger difference. This is due to a small difference between the ideal and effective noise models. The smallness of the error is still a rather surprising result.
In the last case, we study the CNOT decomposition where the bath qubits are target qubits. The simulation is performed for 8 bath qubits.
Now we can see larger differences in the results. This is due to significant changes in the form of the effective noise. It can be shown that here the effective noise model includes strong system-qubit dephasing. We then conclude that in the considered situations noise-utilising system-bath simulations are feasible and that small changes in gate decompositions can lead to large changes in the effective noise model.
Spin coupled to an ohmic bath
This model is a cornerstone of the spin-boson theory. It shows how system-bath dynamics can drastically change with system-bath interaction strength. Here the strength is characterized by only one parameter \(\alpha\) (the so-called Kondo parameter). As a rough overall picture, for \(\alpha\ll 1\), the system dynamics show damped oscillations, whereas for \(\alpha\lesssim 1/2\), the dynamics transform into slow incoherent relaxation. For \(\alpha > 1\) and \(T=0\) the system does not relax.
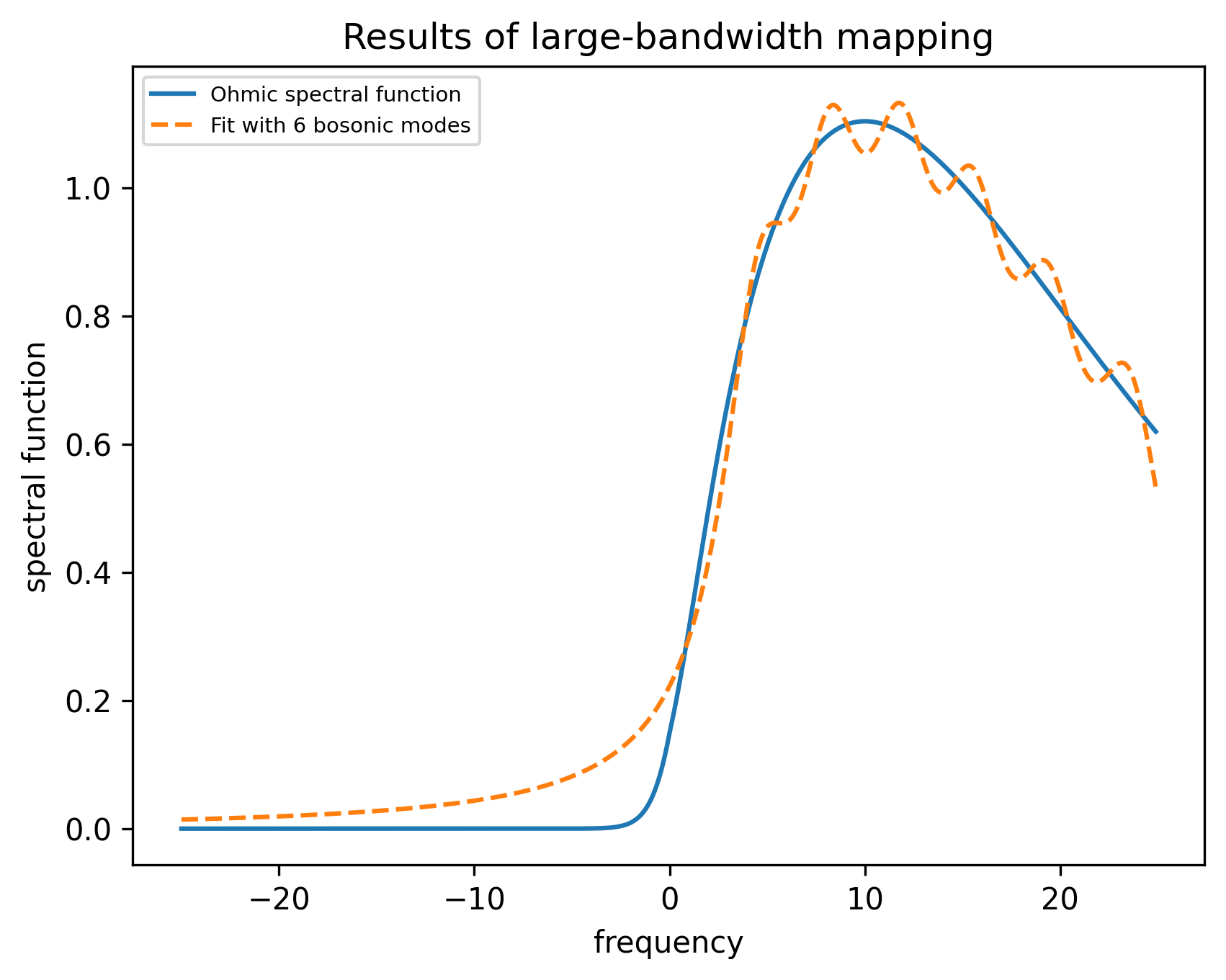
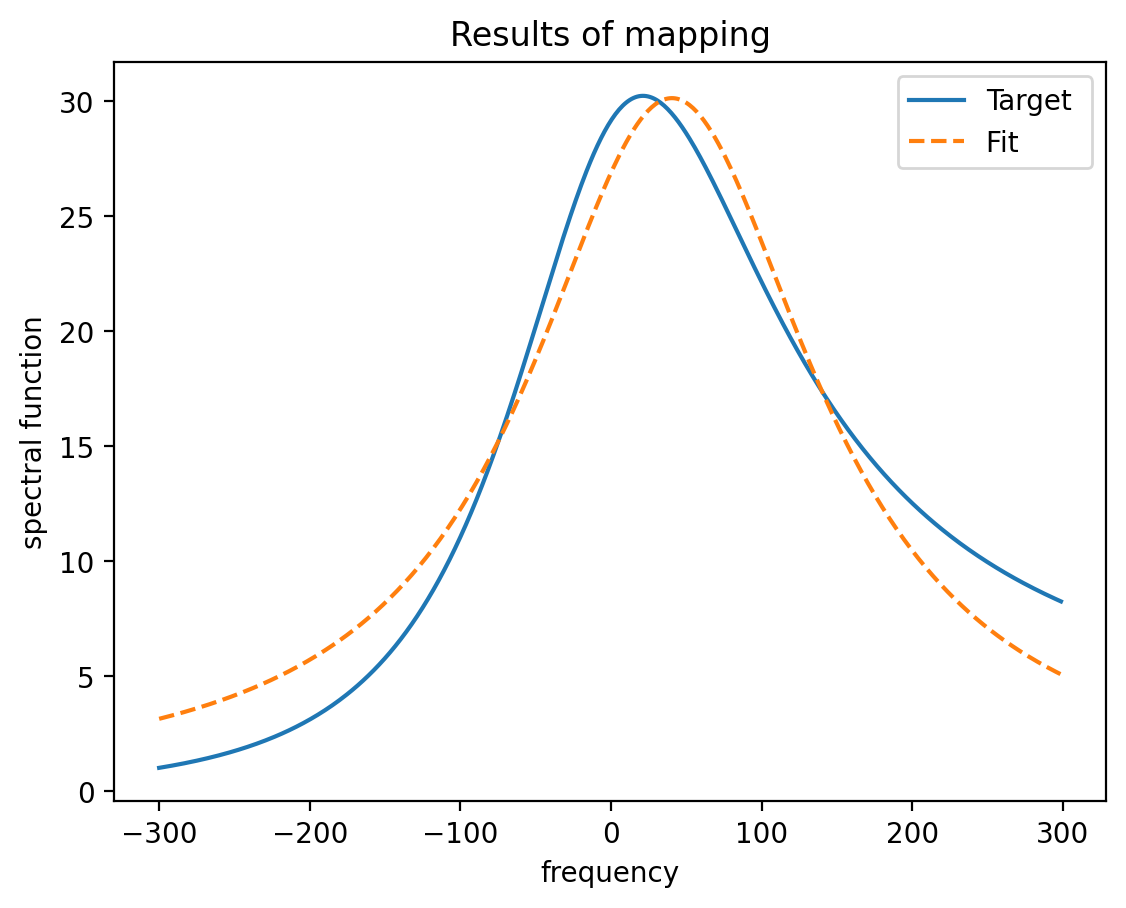
Using the system-bath tool, we can demonstrate this transition with a coarse grained bath (at a finite temperature). Below we consider a spectral function
\[ \begin{align} \Delta &= 1 \\ S(\omega) &= \frac{2\alpha\omega}{1 - \exp(-\omega / T) } \exp(-\vert \omega\vert / \omega_c) \\ \omega_c &= 10 \\ T &= 0.5 \nobreakspace. \end{align} \]
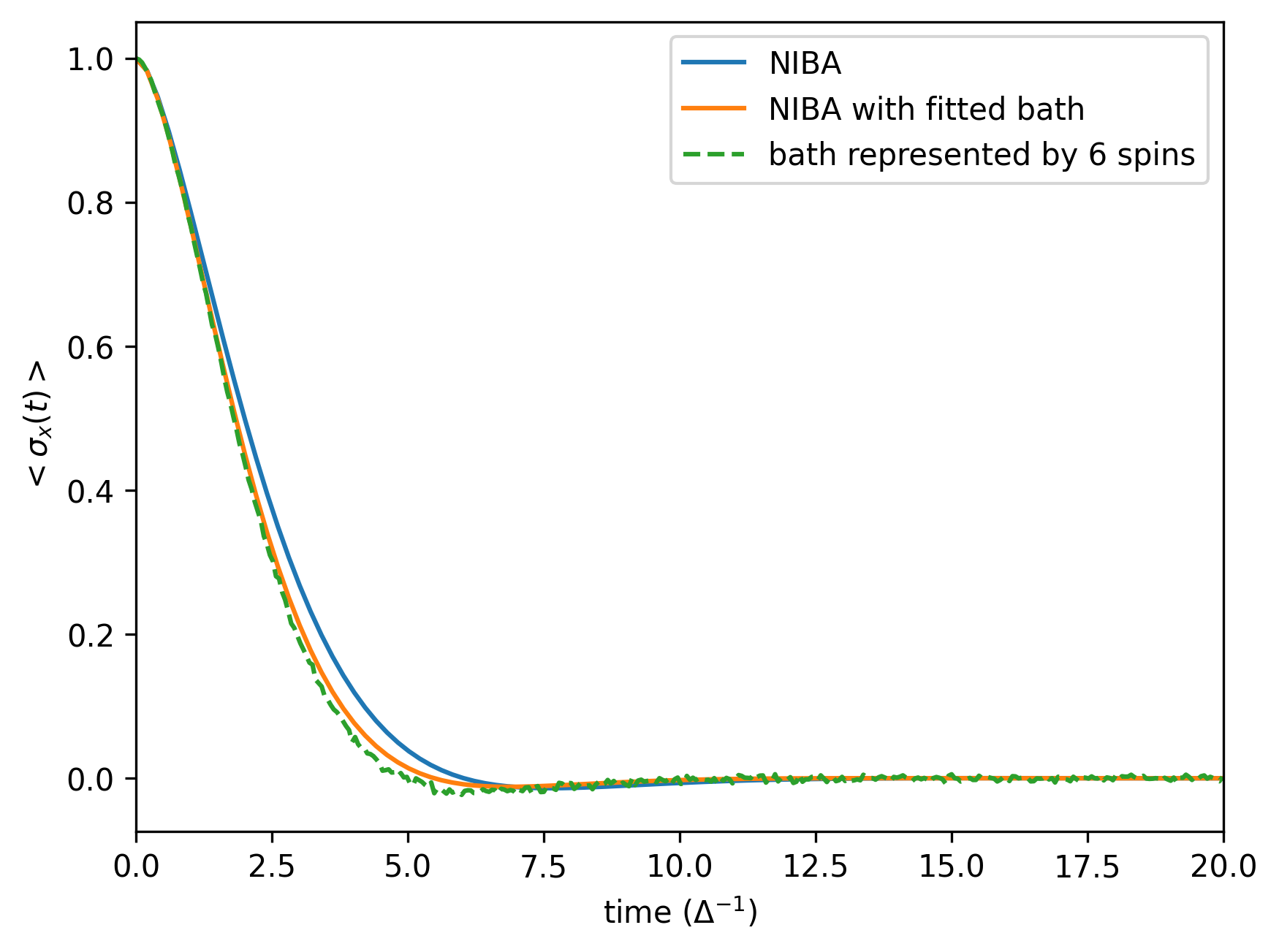
As earlier, we solve the time evolution when initially prepared in the eigenstate +1 of \(\sigma^x_\textrm{system}\). As a "correct" reference result, we use the so-called NIBA (non-interacting blip approximation) calculation, performing it with the original correct bath and with the coarse-grained baths. (The NIBA calculation is made by a piece of code not provided in the HQS Noise App.) The coarse-graining is performed by optimizing parameters of 8 bath modes having the same widths.
Below, we show the results for quantum simulation with variable-MS decomposition for \( \alpha=0.05 \)
for \(\alpha=0.3\)
and for \(\alpha=0.6\)
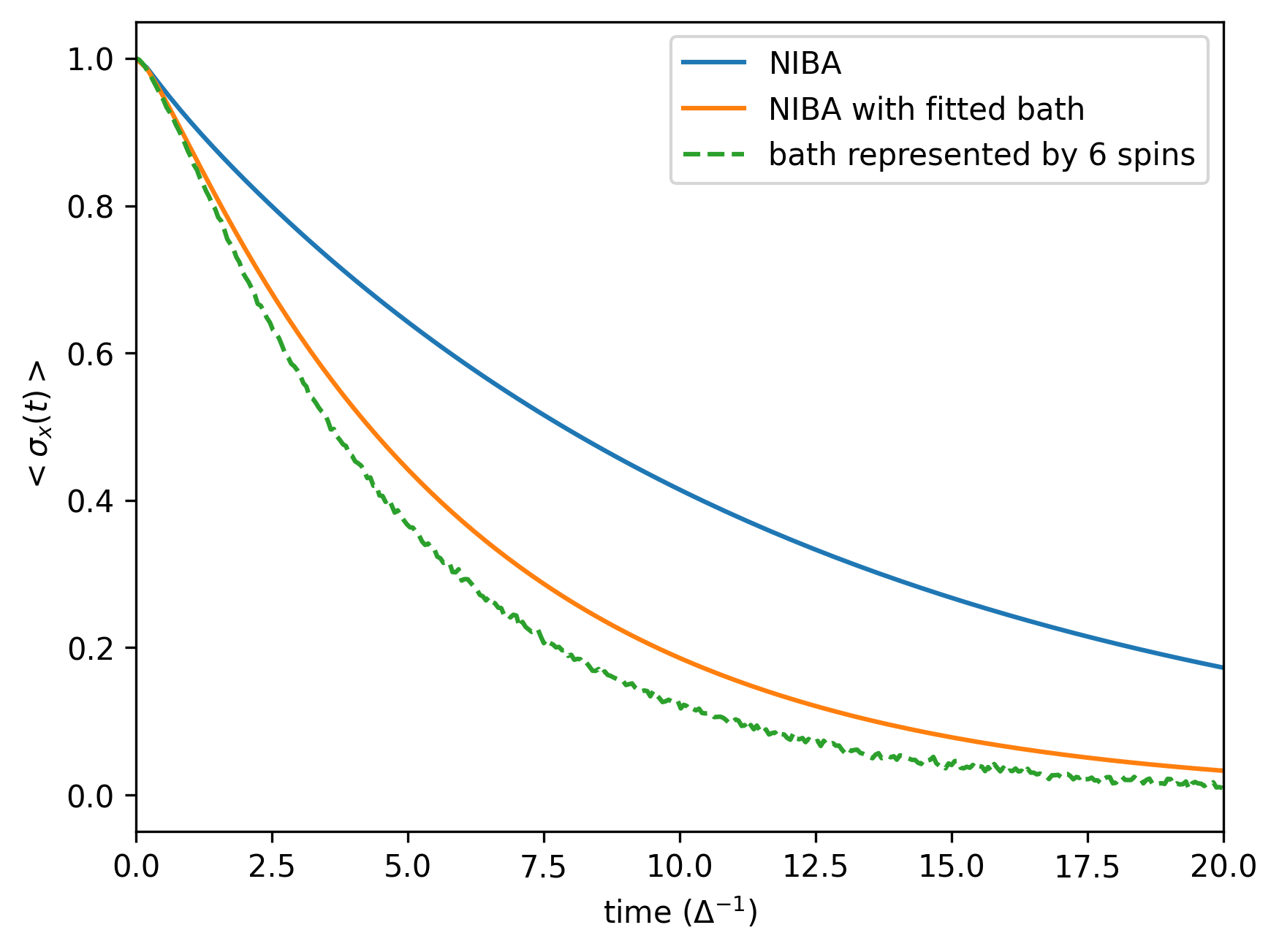
We see the transition from damped oscillations to incoherent decay. The results also agree well with the NIBA solutions. A noticeable difference to the original-bath NIBA result emerges for large \(\alpha\), which is due to increased sensitivity of dynamics to temperature (the effective coarse-grained bath temperature is elevated), rather than an increase in bath-spin populations. As this setup is analogous to the previous example, with the difference of distributed bath parameters, the conclusions made for the CNOT decompositions remain the same.
Exciton transport
Exciton transport has been studied extensively using multi-spin boson models. The spins correspond to bacteriochlorophyll pigment molecules. Their electronic excited states interact and can effectively "jump" between different sites. They couple longitudinally to a boson bath, which corresponds to vibrations in the central molecular structure and the surrounding protein. The total Hamiltonian describing this system is of the form:
\[ \begin{align} H &= \sum_{i \in \textrm{system}}\frac{\Delta}{2}\sigma^i_z + \sum_ {i<j \in \textrm{system}} \frac{g_{ij}}{2}\left( \sigma^+_i \sigma^-_j + \sigma^-_j \sigma^+_i \right) \\ &+\sum _{i \in \textrm{system}} \sum _{sm \in \textrm{bath}} \frac{g _{ism}}{2} \sigma^z_i \left[a_s(\omega_m) + a^\dagger_s(\omega_m)\right] + \sum _{sm} \omega_m a^\dagger_s(\omega_m) a_s(\omega_m) \end{align} \] Energy is transferred across a network of 8 spins (or in more general models, 3 sets of 8 spins = 24 spins). This energy transfer occurs with partial energy dissipation in the bath. The environment is often taken to be Ohmic or sub-Ohmic, but in a more detailed simulation it can be allowed to have more structure. Here we choose the Ohmic form of a spectral function:
\[ \begin{align} J(\omega) &= \frac{2}{\pi}\frac{\lambda \gamma \omega}{\gamma^2 + \omega^2} \\ \lambda &= 35~\textrm{cm}^{-1} \\ \gamma &= 110~\textrm{cm}^{-1} \\ T &= 100~\textrm{cm}^{-1} (144~K) \nobreakspace . \end{align} \]
and coarse grain it by 2 broad modes. In the simulation, the scaling of small-angle terms is made exactly in the same way as in the the previous examples. We assume the noise is purely qubit decay.
Furthermore, we greatly simplify the model and consider here a simplified version of the exciton transport model in photosynthesis: a system of 3 spins with system Hamiltonian:
\[ g_{ij\in\textrm{system}} = \begin{pmatrix} 420 & 95 & 0 \\ & 250 & 30 \\ & & 0 \end{pmatrix} \] These are given in units of \(\textrm{cm}^{-1}\).
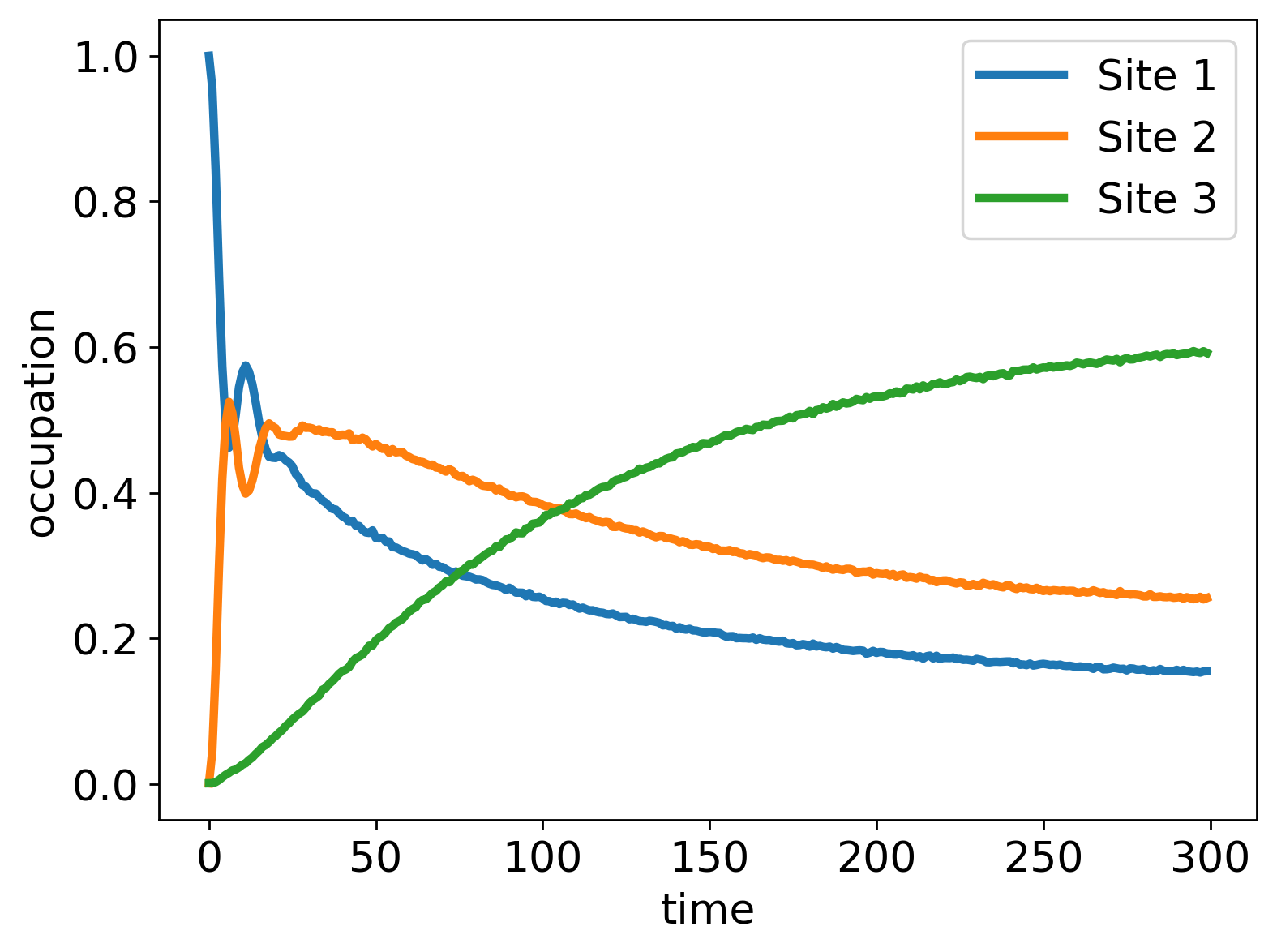
The system is initially left to relax to a steady state where there are no excitations in the system. Then an exciton is inserted on site 1 (by \(\sigma^x\) operation). We then monitor the site populations and study how fast the exciton reaches its destination, site 3:
Even though we include here only 3 sites in the model, the result is very similar to those shown in the literature. This agreement despite such a simple model can be rationalized by noting that the excitation number of spins in the bath stays low, which is also consistent with the results in the literature.
In the second version of the calculation, we add cross correlations to the system-bath interaction. Specifically, we assume here that half of the spectrum seen by sites 1 and 3 is due to coupling to the bath of site 2. The system-bath coupling of spin 2 is kept unchanged as well as the diagonal spectral components of spins 0 and 2.
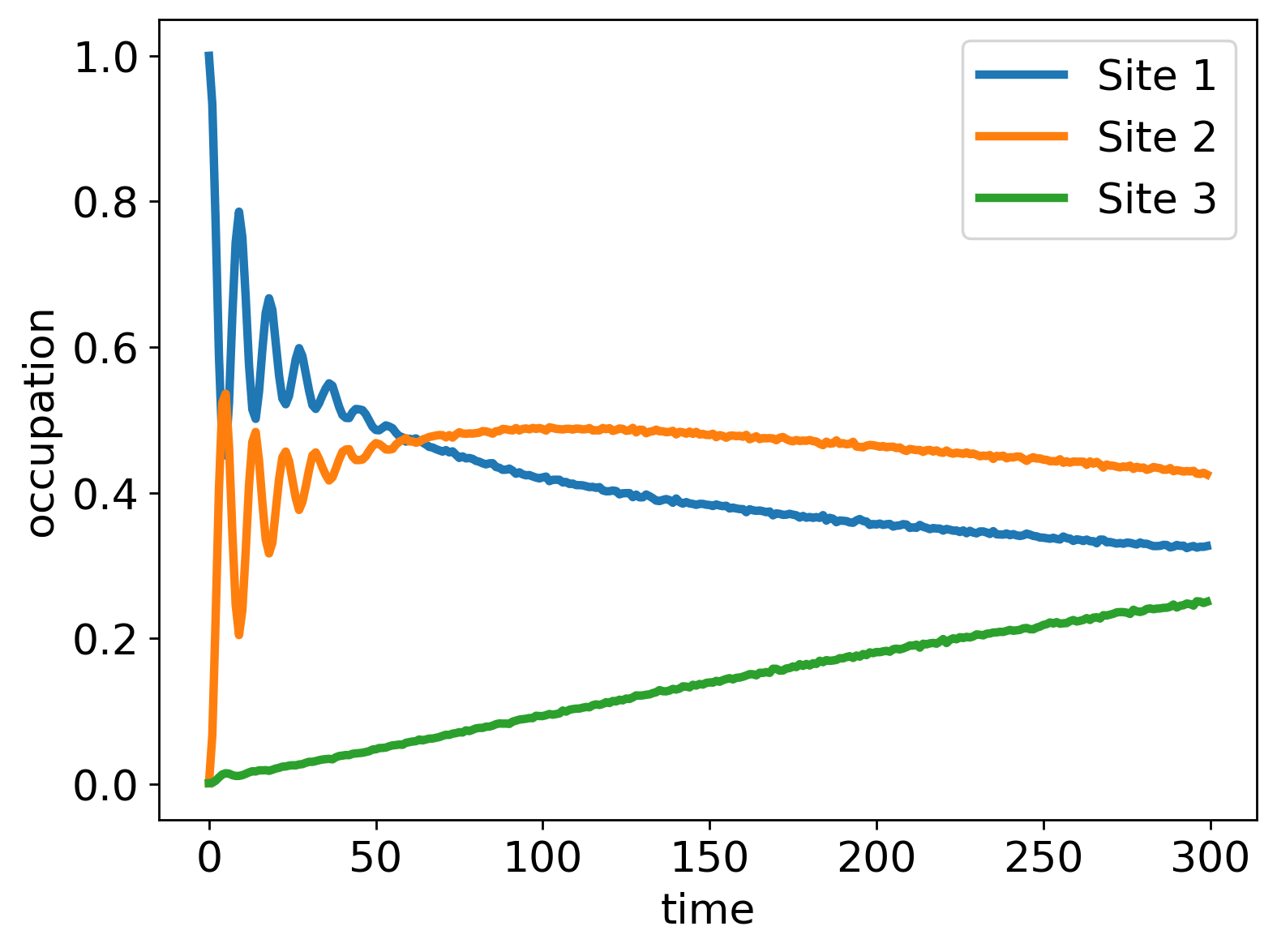
We find relatively strong changes in the solution: the transport to site 3 is essentially weaker. This implies that cross correlations can be harmful for efficient energy transport. The absence of cross-correlations is indeed the usual assumption taken in numerical simulations.