Introduction
HQS Bath Fitter is a tool of HQS Quantum Libraries by HQS Quantum Simulations GmbH to fit a given bath of an open quantum system with an effective bath derived from a set number of bath qubits. It provides a BathFitter Python class that includes several methods specifically for the system-bath analysis, as listed in the Features subsection below.
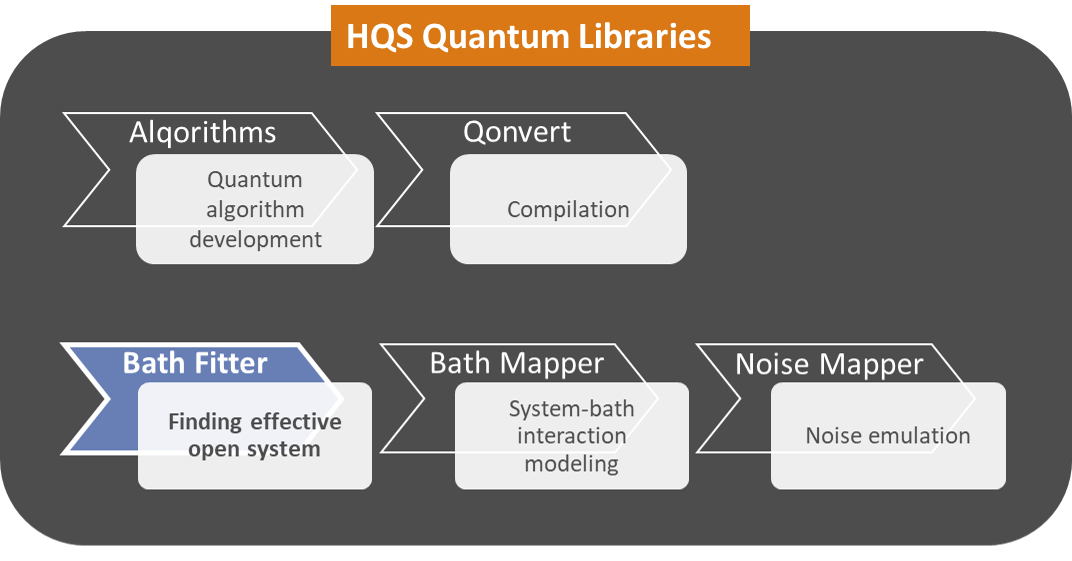
Applications
HQS Bath Fitter is designed to implement complex open quantum systems by approximating their environmental interactions with effective baths. This tool is particularly useful in quantum algorithm development, noise modeling in quantum devices, simulations of open system dynamics, and optimizing the application of Trotterized time evolution in quantum computing. It enables researchers and engineers to translate physical noise environments into compact, efficiently simulatable models, and offers interoperability with other HQStage modules for end-to-end quantum simulation workflows.
A representative application is the fitting of an Ohmic spectral function when a spin system is coupled to an Ohmic bath. The case of an Ohmic bath arises in many areas of physics and highlights how the system-bath dynamics can drastically change depending on the system-bath coupling strength.
Another, more complex, application involves fitting a highly structured (peaked) target spectral function like it arises in noise environments containing so called two level systems — demonstrating the library’s flexibility in handling diverse modeling scenarios.
Interested readers may refer to Figures 2 and 5 in our publication for sample results from these applications.
Getting started
HQS Bath Fitter is a package of HQS Quantum Libraries that can be used in conjunction with other HQStage modules by HQS Quantum Simulations GmbH. To install this module run
hqstage install hqs-quantum-libraries
For a code snippet how to start using HQS Bath Fitter please refer to the usage section. For an expanded collection of examples please see the examples section.
Features
HQS Bath Fitter Library provides the following functions to finding an effective open system, i.e. expressing a target bath with helper qubits.
fit_boson_bath_to_boson_bathfit_spin_bath_to_boson_bathfit_boson_bath_to_fermion_bathfit_spin_bath_to_fermion_bathfit_boson_bath_to_spectral_functionfit_spin_bath_to_spectral_functionspin_bath_trotterstep_from_boson_bath
For further information, the API documentation can be found here.
Further reading
The HQS Bath Fitter is based on our paper describing a quantum algorithm for solving open system dynamics on quantum computers using noise.
Usage
A BathFitter instance is created as follows
from hqs_noise_app import BathFitter
bath_fitter = BathFitter(
number_boson_modes=2,
spins_per_bosonic_mode=1,
broadening_constraint=[0.1, 0.1],
background_broadening_ratio=0.1,
minimum_eigenfrequencies=-2,
maximum_eigenfrequencies=2,
fitting_window=(-0.5, 1, 10),
# specified if we are fitting a system-bath with a spin system
coupling_types=["X"],
max_fitting_iterations=5,
max_fitting_error=0.05,
)
# Print docstring of a function in BathFitter
help(bath_fitter.fit_spin_bath_to_boson_bath)
The parameters of BathFitter are:
number_boson_modes: Number of bosonic modes used for the fit of bosonic bathsspins_per_bosonic_mode: Number of spin modes used to represent one bosonic mode.broadening_constraint(Optional[List[float]]): The optional broadening constraints. When set toNone, broadenings of bosonic modes are fitted freely. When given as a list, the relative broadening of all modes is fixed and only a prefactor is fitted. The prefactor corresponds to the Trotter timestep in a quantum cirucit.background_broadening_ratio(float): Adds a constant background offset to the diagonal spectral functions when fitting. Given as a ratio of the average broadening.minimum_eigenfrequencies(Optional[float]): Minimal value allowed for bath eigenfrequencies.maximum_eigenfrequencies(Optional[float]): Maximum value allowed for bath eigenfrequencies.fitting_window(Optional[Tuple[float, float, int]]): The frequency window used for the fitting (start, end, steps). If no values are provided, the functions uses the whole frequency range to determine the fit.coupling_types(Optional[Union[Dict[Tuple[int, int], List[str]], List[str]]]): A list of the couplings to include (only relevant for spin systems). If None, all the couplings are used: X, Y, Z. The user can also specify this input as a dictionary, where the keys are pairs of indices (system spin index, bath boson index), and the values are the list of couplings (X, Y, Z) which apply to these indices.coupling_indices(Optional[List[Tuple[int, int]]]): A list of allowed fermionic hopping operators of the form \(c^\dagger_j c_k\) that are allowed to couple to bosonic modes (only relevant for fermionic systems). For example[(0,0), (0,1)]only allows coupling operators \(c^\dagger_0 c_0\) and \(c^\dagger_0 c_1\).max_fitting_iterations(int): The number of retries allowed when fitting the spectrum.max_fitting_error(float): The maximum allowed fitting error in fitting the spectrum.
The HQS Bath Fitter uses a simple metric for the quality of the fit: Let \(A\) be the sum of squares of the difference between the fitter and target and \(B\) be the sum of squares of the fitted spectral function. The quality of the fit is defined as the ratio \(\frac{A}{B}\) where a small ratio corresponds to a good fit. By default, a deviation of 5% is allowed. If the criterion is not met, the fitting is retried and if the number of retries exceeds the maximum the fit fails. By default, the number of retries is 5.
More information about the input arguments and the returned systems can be obtained from
help(bath_fitter.fit_spin_bath_to_boson_bath) for example.
More examples on how to use the BathFitter and different functions are in the examples
section.
Examples
Simple example fit_boson_bath_to_boson_bath
In the following, we give an example of the basic usage of the function
fit_boson_bath_to_boson_bath. We would like to fit a spin-boson model to a boson bath. First we
create a mixed Hamiltonian consisting of a spin- and a boson system.
from struqture_py import mixed_systems, spins, bosons
# Number of bosons and spins.
number_system_spins = 1
number_bosons = 2
# Boson energies and broadening.
bath_energies = [0.5, 1.5]
bath_broadenings = [0.1, 0.2]
# Coupling between system and boson.
system_boson_couplings = [0.3, 0.1]
# Create a new mixed system with one spin and one boson subsystem
spin_boson_hamiltonian = mixed_systems.MixedLindbladOpenSystem(
1,
1,
0,
)
# Set bath energies
for bath_index, bath_energy in enumerate(bath_energies):
index = mixed_systems.HermitianMixedProduct(
# Identity spin operator
[spins.PauliProduct()],
# Create a Boson occupation operator
[bosons.BosonProduct([bath_index], [bath_index])],
[],
)
spin_boson_hamiltonian.system_add_operator_product(index, bath_energy)
# Set bath noise
for bath_index, bath_broadening in enumerate(bath_broadenings):
# create the index for the Lindblad terms.
# We have pure damping
index = mixed_systems.MixedDecoherenceProduct(
# Identity spin operator
[spins.DecoherenceProduct()],
# Create a Boson occupation operator
[bosons.BosonProduct([], [bath_index])],
[],
)
spin_boson_hamiltonian.noise_add_operator_product((index, index), bath_broadening)
# Set couplings, use longitudinal (Z) coupling
for bath_index, system_bath_coupling in enumerate(system_boson_couplings):
index = mixed_systems.HermitianMixedProduct(
# Identity spin operator
[spins.PauliProduct().z(0)],
# Create a Boson coupling operator (always a + a^dagger)
[bosons.BosonProduct([], [bath_index])],
[],
)
spin_boson_hamiltonian.system_add_operator_product(index, system_bath_coupling)
Now we can fit the spin_boson_hamiltonian to a boson bath with fit_boson_bath_to_boson_bath by
import numpy as np
from hqs_noise_app import BathFitter
# create spectrum from Spin-Bath-System
min_frequency = -2
max_frequency = 4
number_frequencies = 1000
frequencies = np.linspace(min_frequency, max_frequency, number_frequencies)
bath_fitter = BathFitter(
number_boson_modes=2,
spins_per_bosonic_mode=1,
broadening_constraint=[0.1, 0.1],
background_broadening_ratio=0.1,
minimum_eigenfrequencies=-2,
maximum_eigenfrequencies=2,
fitting_window=(-0.5, 1, 10),
coupling_types=["Z"],
)
fitted_spin_boson_system, _ = bath_fitter.fit_boson_bath_to_boson_bath(
original_system=spin_boson_hamiltonian,
frequencies=frequencies,
number_spins=number_system_spins,
)